guyvsdcsniper
- 264
- 37
- Homework Statement
- Using energy considerations, calculate the distance between centers of the palladium nuclei just after fission,when they are momentarily at rest.
- Relevant Equations
- E=K+Eo
I am trying to solve part b of this problem. I know the particles are moving at first and are at rest right after fission per the question.
Using the relativistic Kinetic Energy equation and the energy between two charges I believe I can solve for r, the radius between the two charges.
I am a bit lost on what the V should be on the kinetic energy side. Would it be the answer I got from A? I don't think that makes much sense since I derived the V w/o the relativistic Kinetic equation because the speed was very low.

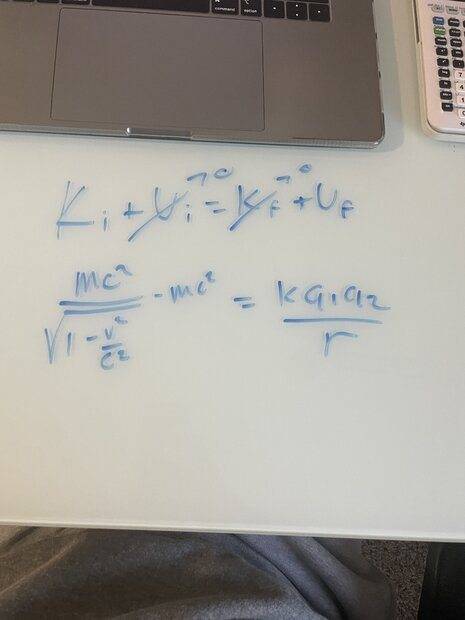
Using the relativistic Kinetic Energy equation and the energy between two charges I believe I can solve for r, the radius between the two charges.
I am a bit lost on what the V should be on the kinetic energy side. Would it be the answer I got from A? I don't think that makes much sense since I derived the V w/o the relativistic Kinetic equation because the speed was very low.