Finding the eigenvalues of a 3x3 matrix

[uzman1243]

Homework Statement

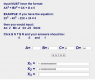
A =
7 -5 0
-5 7 0
0 0 -6

Can you please show your method aswell. Every time I try I get the wrong answer.

FYI Eigen values are 12.2,-6

The Attempt at a Solution

so far I got:
det =
7-λ -5 0
-5 7-λ 0
0 0 -6-λ

Im unsure what to do next. I tried doing this
(7-λ) [(7-λ)*(-6-λ)] - (-5)(-5(-6-λ)) + 0 = 0
but when I expand and get a cubic equation and solve it, i don't get the right answer which is 12,2,-6

 

[SteamKing]

Show us your cubic equation in λ after you have done the algebra and collected all the terms. You may have made a mistake in your calculations.

 

[uzman1243]

Show us your cubic equation in λ after you have done the algebra and collected all the terms. You may have made a mistake in your calculations.

continuing from (7-λ) [(7-λ)*(-6-λ)] - (-5)(-5(-6-λ)) + 0 = 0


(7-λ) [(7-λ)*(-6-λ)] + 5 (30+5λ) = 0
(7-λ) [(7-λ)*(-6-λ)] +150 + 25λ = 0
(7-λ) [-42-λ+λ^2] + 150 + 25λ = 0

294 - 7λ + 7λ^2 + 42λ + λ^2 - λ^3 + 150 +25λ = 0

444 + 60λ +8λ^2 - λ^3 = 0

So i checked that with the calculator and the answer is completely off.
Also in my first semester exam we aren't allowed to use the calc. so i need to find another way to solve the cubic equation OR instead do some sort of manipulation of the initial det matrix and get the answer from there.

Any ideas?
and thank you

 

[The Electrician]

continuing from (7-λ) [(7-λ)*(-6-λ)] - (-5)(-5(-6-λ)) + 0 = 0


(7-λ) [(7-λ)*(-6-λ)] + 5 (30+5λ) = 0
(7-λ) [(7-λ)*(-6-λ)] +150 + 25λ = 0
(7-λ) [-42-λ+λ^2] + 150 + 25λ = 0

294 - 7λ + 7λ^2 + 42λ + λ^2 - λ^3 + 150 +25λ = 0

444 + 60λ +8λ^2 - λ^3 = 0

So i checked that with the calculator and the answer is completely off.
Also in my first semester exam we aren't allowed to use the calc. so i need to find another way to solve the cubic equation OR instead do some sort of manipulation of the initial det matrix and get the answer from there.

Any ideas?
and thank you

Looks to me like you should have:

-144 + 60λ +8λ^2 - λ^3 = 0

 

[SteamKing]

continuing from (7-λ) [(7-λ)*(-6-λ)] - (-5)(-5(-6-λ)) + 0 = 0


(7-λ) [(7-λ)*(-6-λ)] + 5 (30+5λ) = 0
(7-λ) [(7-λ)*(-6-λ)] +150 + 25λ = 0
(7-λ) [-42-λ+λ^2] + 150 + 25λ = 0

294 - 7λ + 7λ^2 + 42λ + λ^2 - λ^3 + 150 +25λ = 0

444 + 60λ +8λ^2 - λ^3 = 0

So i checked that with the calculator and the answer is completely off.
Also in my first semester exam we aren't allowed to use the calc. so i need to find another way to solve the cubic equation OR instead do some sort of manipulation of the initial det matrix and get the answer from there.

Any ideas?
and thank you

Check your cubic polynomial again. You have an arithmetic error in calculating the constant term.

Here's a tip: when you have something like (7-λ)(7-λ)(-6-λ), evaluate the two identical terms first (7-λ)(7-λ) = 49 - 14λ + λ^{2}, since you should be able to write the square of a monomial by doing a mental calculation.

Alternately, when you want to calculate the determinant of a matrix with several zeroes in a single row or column, like the matrix in this problem, using minors might save you considerable calculation.

In any event, when you obtain the proper cubic characteristic equation, you can use several different methods to find the solutions: you can guess a solution, you can use the rational root theorem, or you can plot the equation.

 

[AlephZero]

continuing from (7-λ) [(7-λ)*(-6-λ)] - (-5)(-5(-6-λ)) + 0 = 0

The factor (-6-λ) is in both terms. So you can simplify this to
[ (7-λ)(7-λ) - (-5)(-5) ] (-6-λ) = 0
and save a lot of work.

And (7-λ)(7-λ) - (-5)(-5) is of the form $a^2 - b^2$, so you should be able to factorize it without multiplying everything out.

 

[uzman1243]

Looks to me like you should have:

-144 + 60λ +8λ^2 - λ^3 = 0

Oh yeah. But sill I used the values you got and I checked with an online cubic calculator, and this is what I got

The answer is quite close. x1 should be 12 and x2 should be -6.

can you explain why this is so??

 

[uzman1243]

The factor (-6-λ) is in both terms. So you can simplify this to
[ (7-λ)(7-λ) - (-5)(-5) ] (-6-λ) = 0
and save a lot of work.

And (7-λ)(7-λ) - (-5)(-5) is of the form $a^2 - b^2$, so you should be able to factorize it without multiplying everything out.

That is awesome. But i don't get how you were able to factorize it WITHOUT multiplying it out?

 

[Mark44]

And (7-λ)(7-λ) - (-5)(-5) is of the form $a^2 - b^2$, so you should be able to factorize it without multiplying everything out.

That is awesome. But i don't get how you were able to factorize it WITHOUT multiplying it out?

AlephZero explained where the factorization comes from. If a = 7 - λ and b = -5, then (7-λ)(7-λ) - (-5)(-5) = a² - b², so you can factor it as (a - b)(a + b) or as (7 - λ - (-5))(7 - λ + (-5)).