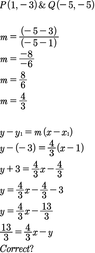- #1
mathdad
- 1,283
- 1
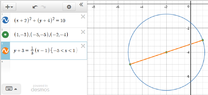
Determine the equation of the circle in standard form, given the coordinate of the diameter PQ.
P(1, -3) and Q(-5, -5)
View attachment 7471
P(1, -3) and Q(-5, -5)
View attachment 7471
Attachments
Last edited by a moderator: