LT72884
- 335
- 49
Ok, so i have done many math classes, as i am an engineer, however, a theory class and proof class i h ave not done, except maybe one haha.
here is my question, if i draw some sort of curved line by hand, how do i find an equation for that?
for example, i draw half of a tear drop but along the horizontal (like the posted image). How would i find the equation of that line, preferably without a computer? im just wanting to see how this was done back in the past.
thanks
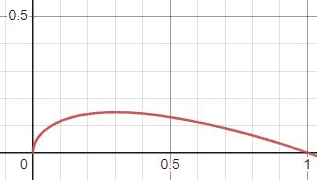
here is my question, if i draw some sort of curved line by hand, how do i find an equation for that?
for example, i draw half of a tear drop but along the horizontal (like the posted image). How would i find the equation of that line, preferably without a computer? im just wanting to see how this was done back in the past.
thanks