Finding the equation of this tangent

[Firepanda]

I have this graph

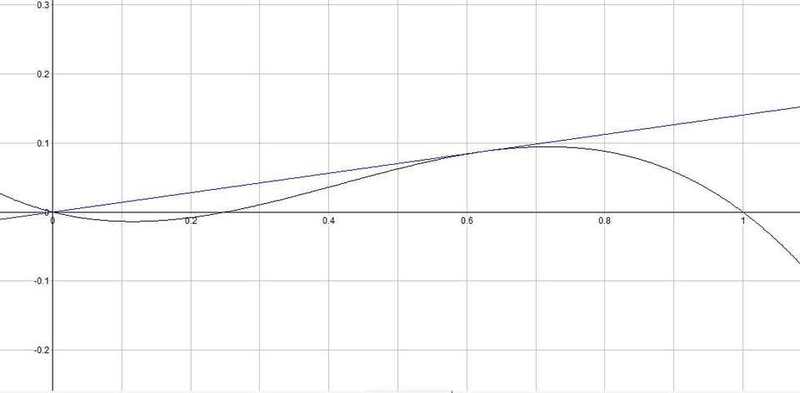
The blue line is a tangent to the black

The blue line starts at (0,0)

I need to show that the blue line y=Hx is a tangent to the black line y= x(x-L)(1-x), (0<L<1)

By deducing that H = (1-L)²/4

I took the example L=0.25 in the pic, where H = 9/64 where it's a tangent, and it's like that for any L I choose between 0 and 1

But how can I deduce that H = (1-L)²/4?

I differentiated my function y' = 2x - 3x² - L + 2xL and I equated it to H but that got me nowhere..

Any help?

Thanks

 

[Mark44]

What information is given in this problem? What does L represent? Are you given that y = x(x - L)(1 - x)? The slope of the tangent line looks to me to be closer to 1/7.

 

[Firepanda]

What information is given in this problem? What does L represent? Are you given that y = x(x - L)(1 - x)? The slope of the tangent line looks to me to be closer to 1/7.

L is a parameter bounded between 0 and 1

I chose it as 0.25 just to represent the graph

The slop is (1-L)²/4 = (3/4)²/4 = (9/16)/4 = 9/64

That's all the information I have, and yes I was given the equation of the curve

 

[Mark44]

You're supposed to deduce that H = (1 - L)²/4; you can't just use it. How did you get the equation of the curve, which you show as y = x(x - L)(1 - x)? Were you given that equation, or did you get it from looking at the graph?

 

[Firepanda]

You're supposed to deduce that H = (1 - L)²/4; you can't just use it. How did you get the equation of the curve, which you show as y = x(x - L)(1 - x)? Were you given that equation, or did you get it from looking at the graph?

I'm aware I can't just use it I was just trying to represent it to everyone that this H is the gradient of the line tangent to the curve and passing through (0,0) and also show to myself what H was doing.

I was given the equation yes, perhaps if I put up the whole question it might be easier.

I'm trying to do part iii)

I had the graph as shown, i plotted for some value of L the H_cx and f(x), as shown also. This shows it's a tangent line, and a bifurcation. But of course this isn't deducing anything, I'm wondering how I can do this.

 

[Firepanda]

Ok no worries I have the answer I believe

 

[Mark44]

That's more like it. There's some technical jargon used here that I don't understand - bifurcation. I know what the word means, but I'm not sure what it means in relation to this problem.

Anyway, here are some ideas you might be able to use. In part ii of the problem, harvesting is back in, so you have dx/dt = x(x - L)(1 - x) - Hx. Graphically this represents the signed difference of the y coordinates on the straight line minus those on your cubic.
Multiplying through, I get
dx/dt = -x³ + (L + 1)x² - (L + H)x
= -x(x² - (L + 1)x + (L + H))

dx/dt = 0 ==> x = 0 or x² - (L + 1)x + (L + H) = 0
In the quadratic, we have
$$x~=~\frac{L + 1 \pm \sqrt{(L + 1)^2 - 4(L + H)}}{2}$$
$$=~\frac{L + 1 \pm \sqrt{L^2 - 2L + 1 -4H)}}{2}$$
$$=~\frac{L + 1 \pm \sqrt{(L - 1)^2 -4H)}}{2}$$

Apparently we want the quantity under the radical to be zero. I'm not sure why, but if that's the case, what you're trying to deduce about H just falls out. Presumably you're more familiar with the fine points of this problem, and you can come up with an explanation of why this works.

Notice that I've been working the whole time with dx/dt. At no point did I take the derivative of anything or integrate anything. The problem involves looking at dx/dt as a function in its own right and saying something about it.

 

[Firepanda]

Yep exactly how I found it! Looked back through my answer to part ii) and it became obvious it's to do with my roots.

Thanks a lot!