Engineering Finding the force acting on a point charge with a disk around it

[falyusuf]

Homework Statement

Attached below.

Relevant Equations

Given below.

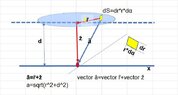
Question:

Here's my attempt with the relevant equations:

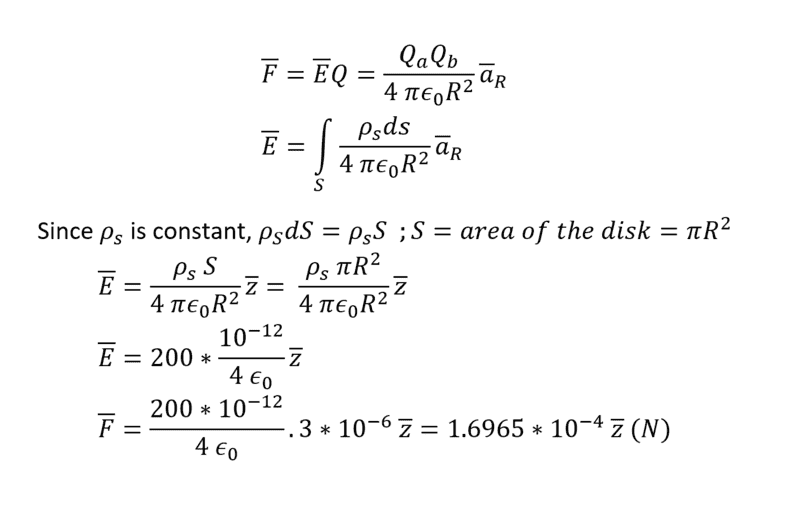
The correct answer is F = -99.4 az μN. Could someone please figure out my mistake?

 

[Gordianus]

Let's consider the second equation (E=...). What does R stand for?

 

[falyusuf]

Let's consider the second equation (E=...). What does R stand for?

Radius.

 

[Gordianus]

Hmmm...Try again

 

[Babadag]

The position of the disk in space is not clear. What does it mean "a disk located 0<ρ<1 " that is, the center of the disk is in the z axis or is displaced by 1 m and the radius of the circle is 1 m or only 1/2 m. It is not clear at all.

 

[Babadag]

I think I got how was calculation done. The circle of radius 1m with the center located on z axe. If we consider an infinite small surface dS=r*dα*dr [as in attached sketch] then:
dE=ρs/(4/PI()/εo/a^3*dS*ā
E=ρs/(4/PI()/εo*ʃdS*ā/sqrt(r^2+d^2)/(r^2+d^2)
E=ρs/(4/PI()/εo*ʃdS*ā/(r^2+d^2)^3/2
E=ρs/(4/PI()/εo*ʃʃdr*r*dα*ā(r^2+d^2)^3/2 [one integral for dr and another for α]
The component radial ȓ is cancel out, because of all direction of component radial ȓ around z
E=2*pi()*ρs/4/PI()/εo*ʃdr*r*ž/(r^2+d^2)^3/2 |ž|=d
E=ρs/2/εo*d*ʃdr*r/(r^2+d^2)^3/2
Let’s put x=r^2+d^2 then dx=2*r*dr or r*dr=dx/2 ; r=0 x=1 r=1 x=2
ʃdx/2/x^3/2=1/2/(-3/2+1)*x^(1-3/2)=-1/x^0.5|x=1 to x=2|
-1/sqrt(2)+1/sqrt(1)= 0.292893
E=ρs/2/εo*d*0.292893=3.313269 V/m
F=3.313269*30=99.39808 µN