Finding the frequency of a string based on Mass and Tension

In summary, the conversation discusses a problem involving finding the frequency of a string using a specific formula. The solution is provided using values for tension, linear mass density, and string length. There is confusion about the calculation and whether or not to divide by 2L. Additionally, there is a question about the string's ability to vibrate freely over its entire length.
  • #1
SoundsofPhysics
2
0
Thread moved from the technical forums to the schoolwork forums
I saw the following problem in a test I was reviewing:
1641660422506.png

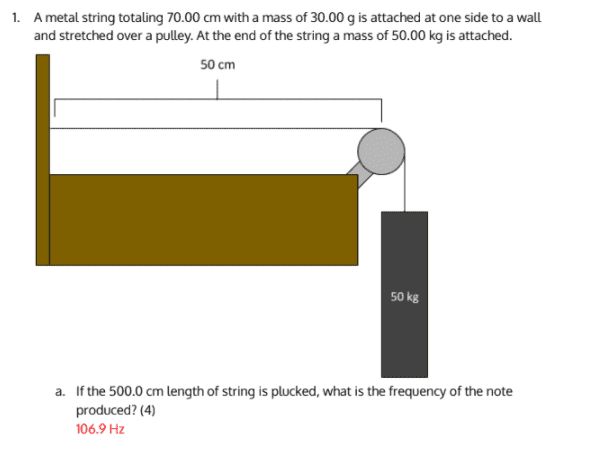
I don't understand how they got their answer. I used the formula: ƒ=sqrt(T / u) / 2L where f is the frequency of the string, T is the tension, u is the linear mass density, and L is the length of the string.
I got:
T = mg = 50 * 9.8 = 490N
u = m/l = 3/7 g/cm = 0.04285 kg/m
L = 70cm = 0.7m
Therefore f = sqrt(490 / 0.04285) / 1.4 = 106.93 / 1.4 = 76.38Hz. I see that they got their answer from the first part, but did they forget to divide by 2L, or was I not supposed to do that? Thanks!
 
Physics news on Phys.org
  • #2
Can the wave freely vibrate over the entire 70 cm length? Think about what happens at the pulley.
 

FAQ: Finding the frequency of a string based on Mass and Tension

How do you calculate the frequency of a string based on mass and tension?

The frequency of a string can be calculated using the formula f = (1/2L) * √(T/m), where L is the length of the string, T is the tension applied to the string, and m is the mass per unit length of the string.

Why is mass and tension important in determining the frequency of a string?

Mass and tension are important because they affect the properties of the string, such as its stiffness and density, which in turn determine the frequency at which the string will vibrate.

Can the frequency of a string change if the mass and tension are altered?

Yes, the frequency of a string will change if the mass or tension is altered. Increasing the mass or tension will result in a higher frequency, while decreasing them will result in a lower frequency.

How does the length of the string affect its frequency?

The length of the string is directly proportional to its frequency. This means that as the length of the string increases, the frequency decreases, and vice versa.

What is the unit of measurement for mass and tension in this calculation?

The unit of measurement for mass is typically grams (g) or kilograms (kg), while the unit for tension is usually measured in newtons (N).

Similar threads

Tension and frequency of a vibrating violin string
Replies
26
Views
6K
Tension in a string which connects 3 pulleys
Replies
12
Views
604
Time it Takes for a Transverse Pulse to Travel a Distance "L" Up a Cable Against Gravity?
Replies
13
Views
766
Waves and vibrations on a string
Replies
2
Views
1K
Which Frequency is NOT Possible for a Vibrating String?
Replies
5
Views
2K
Frequencies of the first three overtones in a string?
Replies
2
Views
1K
Tension in the string while it descends
Replies
8
Views
2K
Tension required to tune a string to the note of ##E_2##
Replies
1
Views
2K
To find the modulus of elasticity of a light elastic string
Replies
7
Views
2K
Standing Waves On Strings: Harmonic and Frequency Problem
Replies
2
Views
4K

Hot Threads

Recent Insights

Back
Top