Heatherirving
- 7
- 0
Hello
I would need help to continue.
calculation problem:
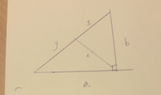
Given a right angled triangle with catheter lengths a and b length units, determine and indicate the length of the bisectris to the right angle.View attachment 6595
find: Xa^2 + b^2 = (y+z)^2X^2 + y^2 = a ^2X^2 + z^2 = b ^2
I would need help to continue.
calculation problem:
Given a right angled triangle with catheter lengths a and b length units, determine and indicate the length of the bisectris to the right angle.View attachment 6595
find: Xa^2 + b^2 = (y+z)^2X^2 + y^2 = a ^2X^2 + z^2 = b ^2
Attachments
Last edited: