Finding the Limit of a Series: Exploring Different Patterns and Approaches

[chwala]

Homework Statement

See attached.

Relevant Equations

Limits

Consider the series below;

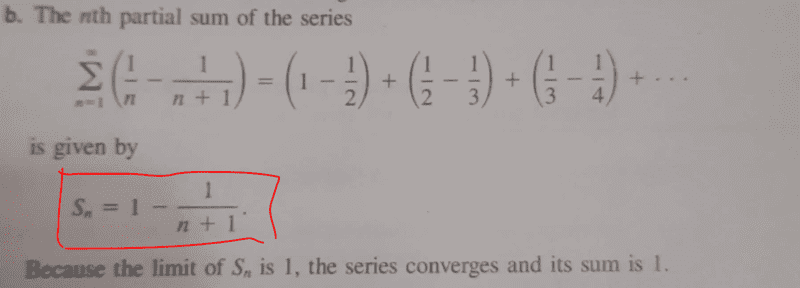
From my own calculations, i noted that this series can also be written as $S_n$=$\dfrac {3}{8}$⋅$\dfrac {4^n}{3^n}$. If indeed that is the case then how do we find the limit of my series to realize the required solution of $1$ as indicated on the textbook? I tried taking limits...L Hopital's rule... and still got $∞$ implying divergence. Are we required to solely maintain the series in the pattern indicated on the text and not any other way?

In other words, if one was given a specific question to find the limit of my series $S_n$=$\dfrac {3}{8}$⋅$\dfrac {4^n}{3^n}$in an exam, then would it be correct to state $∞$?

 

[Office_Shredder]

Your formula is wrong. You probably fit it to the first two values, and didn't check if it matches anything else.

 

[chwala]

Your formula is wrong. You probably fit it to the first two values, and didn't check if it matches anything else.

True it is wrong...i ought to have checked if it applies to the sequence $S_3$...but we could also have
...our series $\dfrac {1}{2}$, $\dfrac {2}{3}$, $\dfrac {3}{4}$,$\dfrac {4}{5},$... as
$S_n$=$\dfrac {n}{1+n}$
Cheers