Finding the limits of a piecewise function

[NP04]

Homework Statement

Determine whether f is continuous at c.
(see image for piecewise function f)

EDIT: Sorry if it is a little blurry that is x^3 in the numerator of the rational function and x^2 in the denominator

Relevant Equations

Basic understanding of limits

Problem Statement: Determine whether f is continuous at c.
(see image for piecewise function f)

EDIT: Sorry if it is a little blurry that is x^3 in the numerator of the rational function and x^2 in the denominator
Relevant Equations: Basic understanding of limits

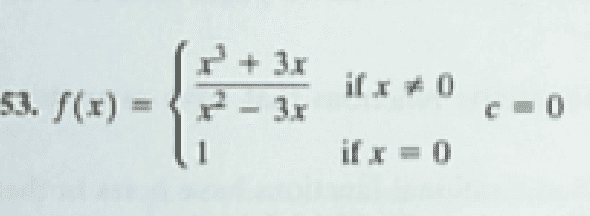
My work:

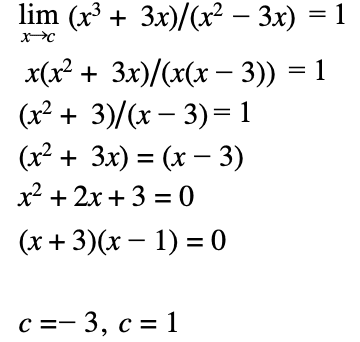
Since the limit as x approaches 1 is equal to 1, for the first piecewise function, the limit of the second piecewise function cannot be equal to 1 otherwise the function would be undefined. Therefore the graph is not continuous as it does not have distinct y values.

Is this the correct reasoning and solution to this problem?

 

[fresh_42]

Problem Statement: Determine whether f is continuous at c.
(see image for piecewise function f)

EDIT: Sorry if it is a little blurry that is x^3 in the numerator of the rational function and x^2 in the denominator
Relevant Equations: Basic understanding of limits

View attachment 244450

My work:
View attachment 244453

Since the limit as x approaches 1 is equal to 1, for the first piecewise function, the limit of the second piecewise function cannot be equal to 1 otherwise the function would be undefined. Therefore the graph is not continuous as it does not have distinct y values.

Is this the correct reasoning and solution to this problem?

No, it is not correct. And you cannot write $\lim_{x\to c}\dfrac{x^3+3x}{x^2-3x} = 1$ for any $c$ as long as you do not know. The interesting limits are those with $x \to 0$ and $x \to 3$ since in both cases the denominator vanishes. Therefore you should start with $$\lim_{\stackrel{x\longmapsto 0}{x\neq 0}}\dfrac{x^3+3x}{x^2-3x} = \ldots $$ and calculate it. Then do the same with $$\lim_{\stackrel{x\longmapsto 3}{x > 3}}\dfrac{x^3+3x}{x^2-3x} = \ldots $$ and $$\lim_{\stackrel{x\longmapsto 3}{0<x < 3}}\dfrac{x^3+3x}{x^2-3x} = \ldots $$

This should give you an idea what happens at these two points.

 

[Mark44]

No, it is not correct. And you cannot write $\lim_{x\to c}\dfrac{x^3+3x}{x^2-3x} = 1$ for any $c$ as long as you do not know. The interesting limits are those with $x \to 0$ and $x \to 3$ since in both cases the denominator vanishes. Therefore you should start with $$\lim_{\stackrel{x\longmapsto 0}{x\neq 0}}\dfrac{x^3+3x}{x^2-3x} = \ldots $$ and calculate it. Then do the same with $$\lim_{\stackrel{x\longmapsto 3}{x > 3}}\dfrac{x^3+3x}{x^2-3x} = \ldots $$ and

Apparently the problem is asking for $\lim_{x \to 0}f(x)$, so it's of no concern what's happening around x = 3.

$$\lim_{\stackrel{x\longmapsto 3}{0<x < 3}}\dfrac{x^3+3x}{x^2-3x} = \ldots $$

This should give you an idea what happens at these two points.

 

[fresh_42]

Apparently the problem is asking for $\lim_{x \to 0}f(x)$, so it's of no concern what's happening around x = 3.

But a good exercise.

 

[MidgetDwarf]

Best approach to gain some intuitive insight is to graph the given function.

 

[epenguin]

But a good exercise.

I'm not sure of that, at least as quoted. If the question is what is the limit of $f(x)$ as $x→0$ why not just ask that? What has this undefined $c$ got to do with anything?

The quoted fraction is obviously discontinuous at $x=3$ and continuous at $x=0$ where its value is -1 and there is nothing special about it; however as the definition of $f$ requires $f(0)$ to be 1, this value is different from the limiting value of the traction as $x→0$ and therefore the function is discontinuous at that point, will that do?

 

[fresh_42]

I used to derive as many properties of a given function, including its graph. I still think that this is a good method to get as many information as possible. And as the given problem is of the kind "introduction to limits", the point $x=3$ serves as a good example that left and right limits don't have to be the same. This makes it a good exercise in the context.

 

[statdad]

You don't need to worry about x = 3 as it wasn't addressed in the question and only adds distraction here.

Just a general statement: when you encounter a rational function (polynomial divided by polynomial) and are asked to investigate a limit, factor the numerator and denominator when possible and cancel any factors common to both. EVEN IF you cancel factors that include the point asked about in the limit you are ok because limit problems investigate what occurs near a point, not at a point.