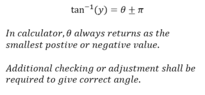Ineedhelpwithphysics
- 43
- 7
- Homework Statement
- In the Picture
- Relevant Equations
- Pythagoras theorem, inverse tan function
So i found the magnitude which is
(-1)^2 + (-2)^2 = P^2 =
Sqrt(5)
Then I used the inverse tan function to find the angle (direction)
theta = arctan (-2/-1) = 63.8 degrees
Im confused with my 63.8 degrees since the angle in the graph looks greater than 63.4 degrees
I subtracted 180 by 63.8 and got 116.6
Since it's going clock wise it's -116.6
Am i right?