Finding the Measure of Angle KPM Using Angle Bisector Theorem

[karush]

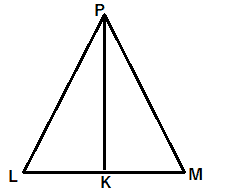
Ray $\overline{PK}$ bisects and the measure of $\angle{LPM}$ is $11x^o$ and the measure of $\angle{LPK}$ is $(4x+18)^o$
What is the measure of
$\angle{KPM}$
$s.\ 12^o \quad b.\ 28\dfrac{2}{7}^o \quad c. \ 42^o \quad d. \ 61\dfrac{1}{5}^o \quad e. \ 66^o$

 

[skeeter]

$\vec{PK}$ bisects $\angle LPM \implies m\angle LPK = m\angle KPM = \dfrac{1}{2} m\angle LPM$

$4x+18 = \dfrac{11x}{2}$

 

[karush]

$\vec{PK}$ bisects $\angle LPM \implies m\angle LPK = m\angle KPM = \dfrac{1}{2} m\angle LPM$

$4x+18 = \dfrac{11x}{2}$

so then
$\angle{LPK} = \angle{KPM} =4x + 18\quad\angle{LPM}=11x$
$\angle{LPK}+ \angle{KPM}= \angle{LPM}$
$4x+18+4x+18=11x$
$8x+36=11x\implies x=12$
$\angle{KPM}=4x+18\quad \therefore \angle{KPM} =4(12)+18=66$
e $66^o$

probably easier than this