andrey21
- 475
- 0
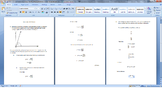
Hi guys, first time poster here. I have been struggling with the following problem for a few days now and could use some guidance. I believe I have the first part correct but the second is causing me trouble (see attachment). Is what I'm doing correct and how would I go about finding the metric tensor?
Thank You in advance for any help :)View attachment 292
Thank You in advance for any help :)View attachment 292