Finding the Minimum θ for Rock Thrown at Speed v_0

[darksyesider]

Homework Statement

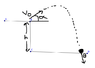
A boy throws a rock at speed v_0 at angle α from a balcony of height h. When the ball hits the ground, its velocity makes an angle θ with the ground. What is the minimum value of θ in terms of h and v_0

Homework Equations

basic kinematics equations.

The Attempt at a Solution

I started out with the following:

$$v_x = v_0 \cos \alpha , v_y = \sqrt{v_0^2\sin^2 \alpha+2gh}$$

Then:

$$f( \theta ) = \tan^{-1} (\frac{\sqrt{v_0^2 \sin^2 \alpha+2gh}}{v_0\cos\alpha}$$

To find the minimum, you have to differentiate, although whenever I do this i get a HUGE expression which doesn't make sense. Any help?Thanks :)

 

[voko]

When $\theta$ is max, $\tan \theta$ is max as well.

 

[darksyesider]

But we need to minimize theta?
Can you please give another hint?

 

[voko]

Ah, sorry. I really meant to say min, not max :)

 

[darksyesider]

Gotcha.

So am I correct in saying that after taking the tangent of both sides, the RHS equals zero? in which case :

$$v_0^2 \sin^2 \alpha = 2gh$$ ??

I attempted it again, however i cannot get rid of alpha here.

 

[voko]

You need $(\tan \theta)' = 0$.

 

[darksyesider]

I still don't get it. Why is that so? Thanks.

 

[voko]

Let $f(x)$ be a monotonic function. Let $g(x)$ be any function. Consider $F(x) = f(g(x))$. $F'(x) = (f(g(x)))' = f'(g(x)) g'(x) = 0$. Because $f(x)$ is monotonic, $f'(x) \ne 0$, thus the previous equation implies $g'(x) = 0$, which means that if $F(x)$ has a stationary point, $g(x)$ has a stationary point there as well.

$\tan$ is monotonic from zero to $\pi/2$.

 

[darksyesider]

So does this mean I have to differentiate $$\frac{\sqrt{v_0^2\sin^2\alpha + 2gh}}{v_0\cos\alpha}$$?
Also, what do i differentiate with respect to? And how do i get rid of alpha? sorry I'm very stuck on this

 

[voko]

Since you are required to find that in terms of $h$ and $v_0$, $\alpha$ has to disappear, which apparently means the minimum must be with respect to it.