- #1
PhysicsKT
- 17
- 0
Here's the problem:
https://i.stack.imgur.com/rUVvu.png

What I did:
[2]: https://i.stack.imgur.com/AX2Ye.png

[3]: https://i.stack.imgur.com/K1Zbi.png
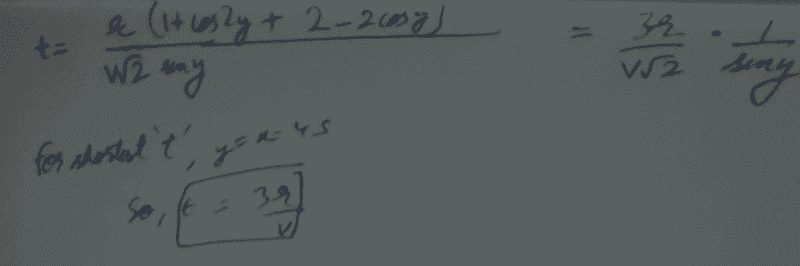
To those who could not understand what I read: So basically I used some geometry to to get $l_1$ and $l_2$ in terms of $r$ and the assumed angle $y$. Now, I assumed that if the ant can climb straight up at a speed $v$, then it should be able to climb up the $l_2$ part with a speed $v \sin{y}$ and similarly for the downward case. Using $t = \frac{l}{v}$ for constant speed, I got $$\boxed{t(y) = \frac{3r}{v\sqrt{2}} \cdot \frac{1}{\sin{y}}}$$. This should be minimised, but minimising this function is not giving me the correct answer. Can someone help me please?
And please post the correct solution you are getting.
https://i.stack.imgur.com/rUVvu.png
What I did:
[2]: https://i.stack.imgur.com/AX2Ye.png
[3]: https://i.stack.imgur.com/K1Zbi.png
To those who could not understand what I read: So basically I used some geometry to to get $l_1$ and $l_2$ in terms of $r$ and the assumed angle $y$. Now, I assumed that if the ant can climb straight up at a speed $v$, then it should be able to climb up the $l_2$ part with a speed $v \sin{y}$ and similarly for the downward case. Using $t = \frac{l}{v}$ for constant speed, I got $$\boxed{t(y) = \frac{3r}{v\sqrt{2}} \cdot \frac{1}{\sin{y}}}$$. This should be minimised, but minimising this function is not giving me the correct answer. Can someone help me please?
And please post the correct solution you are getting.
