Finding the net elongation in a rod due to its own weight

[Hamiltonian]

Homework Statement

A rod of uniform cross-sectional area A and length L has a weight W. It is suspended vertically from a fixed support. If the material of the rod is homogeneous and its modulus of elasticity is Y. then determine the total elongation produced in the rod due to its own weight.

Relevant Equations

$Y = \frac{F/A}{\Delta L/L}$

I realized that the tension in the rod is not uniform and found it to be $T = Wx/L$ I found this by splitting the rod into two sections one of length $x$ and the other of length $L-X$ where x is the length from the base of the hanging rod

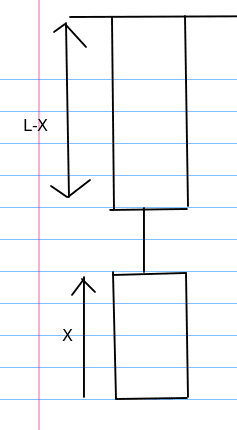
To find the total elongation in the rod I thought we could add up the elongations in tiny segments of the rod of mass $(dm)$ and length $(dx)$ but I am unable to find the extension in the tiny mass

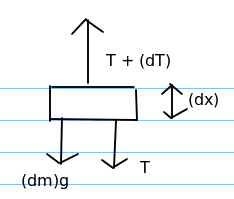
The solution states that the stress at the position of this element is produced by the weight of the length $x$ lying bellow it and therefore stress at this section should be $= Wx/AL$ I am unable to see why the tension acting in the upward direction won't play a role in the extension and since this mass is in equilibrium how exactly do we find which force is producing the elongation $\Delta (dx)$

 

[Lnewqban]

Maximum tension and local elongation occur at the point where $x=L$.
Both values gradually get smaller downwards until reaching the value of zero at the lowest end of the rod.

Any differential portion must have a balance of up and down forces.
If up force is $T_{up}$, down force is $T_{down}+dmg$; therefore, $T_{up}>T_{down}$.

 

[Hamiltonian]

Maximum tension and local elongation occur at the point where $x=L$.

so was my assumption that every $(dm)$ of length $(dx)$ gets elongated by a $\Delta (dx)$ wrong?

Any differential portion must have a balance of up and down forces.
If up force is $T_{up}$, down force is $T_{down}+dmg$; therefore, $T_{up}>T_{down}$.

I think I have stated the exact same in my original post..

 

[Chestermiller]

so was my assumption that every $(dm)$ of length $(dx)$ gets elongated by a $\Delta (dx)$ wrong?I think I have stated the exact same in my original post..

You did it right. $$\frac{dT}{dx}=\frac{mg}{L}$$so$$T=mg\frac{x}{L}=EA\frac{du}{dx}$$where u is the displacement.

 

[haruspex]

The tricky part with questions like this is to be clear what is meant by x. Is it the position of the element dx when the rod is stretched or unstretched? If stretched then the mass density is not uniform.

 

[Chestermiller]

The tricky part with questions like this is to be clear what is meant by x. Is it the position of the element dx when the rod is stretched or unstretched? If stretched then the mass density is not uniform.

X is usually the material coordinate, meaning the original undeformed location of each cross section (measured from the bottom in this problem) in absence of gravitational load. x + u(x) is the corresponding location of the cross section x in the deformed configuration of the rod.

 

[haruspex]

I am unable to see why the tension acting in the upward direction won't play a role

Tension always acts in both directions. It is not so much a force as a pair of equal and opposite forces at each point.
The difference between tension at the lower side of the element and that at the upper side is a second order small quantity for the purpose of finding the strain on the element.

I'm not quite sure how you are using your Δ notation. That's usually a difference, but you seem to be using it as a factor (like, 1+fractional difference).
I recommend using @Chestermiller's notation: x, dx refer to the position and thickness of an element in the unstretched state, while u, du refer to the same element in its stretched state. You then need equations relating: dx, du and T; dx and dT.

 

[Chestermiller]

If x and $x+\Delta x$ are the material coordinates of two neighboring cross sections along the rod (distances measured up from the bottom of the rod prior to hanging the rod), the distances measured up from the bottom of these same two neighboring material cross sections after the rod is hanging under its own weight are $x+u(x)$ and $x+\Delta x+u(x+\Delta x)$, where u is the displacement function (of x) for the cross sections. So the undeformed distance between the two cross sections is $\Delta x$, and the distance between the same two cross sections after the rod extends under its own weight is $[x+\Delta x+u(x+\Delta x)]-[x+u(x)]=\Delta x+u(x+\Delta x)-u(x)$. So the strain in the portion of the rod between the two cross sections is $$\epsilon=\frac{[\Delta x+u(x+\Delta x)]-\Delta x}{\Delta x}=\frac{u(x+\Delta x)-u(x)}{\Delta x}$$In the limit as $\Delta x$ approaches zero, this becomes $$\epsilon(x)=\frac{du}{dx}$$And the stress in the rod at this location is $$\sigma=E\frac{du}{dx}$$where E is Young's modulus of the rod material.

 

[Lnewqban]

so was my assumption that every $(dm)$ of length $(dx)$ gets elongated by a $\Delta (dx)$ wrong?
...

I agree with your statement.
A practical case in which the stress due to the own weight must be considered is the steel rope used in elevators of very tall buildings.

Copied from
https://www.phoenixmodularelevator.com/elevator-ropes/

“Compensating Ropes – Turns out that all of the cable or rope to make an elevator car go up and down is really heavy. This is especially true for really tall buildings. Think about this; a standard one inch elevator cable can weigh 1.85 pounds per foot. As elevator cable makes several trips up and down the hoistway, this weight can really add up. So compensating ropes “compensate” for all the weight of the hoisting ropes on the car or counterweight side. Probably any elevator that exceeds 100′ of travel needs these ropes that are connected to the sling that holds the car and the counterweight frame.”

 

[Hamiltonian]

Tension always acts in both directions. It is not so much a force as a pair of equal and opposite forces at each point.
The difference between tension at the lower side of the element and that at the upper side is a second order small quantity for the purpose of finding the strain on the element.

I'm not quite sure how you are using your Δ notation. That's usually a difference, but you seem to be using it as a factor (like, 1+fractional difference).
I recommend using @Chestermiller's notation: x, dx refer to the position and thickness of an element in the unstretched state, while u, du refer to the same element in its stretched state. You then need equations relating: dx, du and T; dx and dT.

The extension in a tiny mass $(dm)$ of length $(dx)$ is said to have an extension $\Delta (dx)$ I found this notation a bit odd at first but since it was used both by my teacher and my textbook I followed it as well.
Is $u$ supposed to be the position of the mass $(dm)$ in the stretched state and $(du)$ the extension in that element?
also in my notation, I was considering $x$ and $dx$ in the stretched state so I am not sure as to why I would need to care about the position of the element in the unstretched state?

 

[haruspex]

The extension in a tiny mass (dm) of length (dx) is said to have an extension Δ(dx) I found this notation a bit odd at first but since it was used both by my teacher and my textbook I followed it as well.

Ok, I'd not seen that notation before. So what equation can you write for Δ(dx) in terms of dx and T?

Is u supposed to be the position of the mass (dm) in the stretched state and (du) the extension in that element?

Yes.

I was considering x and dx in the stretched state so I am not sure as to why I would need to care about the position of the element in the unstretched state?

If dx is the stretched length of the element then Δ(dx) makes no sense.
If x is the stretched position, how are you going to write an expression for the weight below it in terms of x?

 

[Hamiltonian]

If dx is the stretched length of the element then Δ(dx) makes no sense.
If x is the stretched position, how are you going to write an expression for the weight below it in terms of x?

I think I got a bit confused your right $\Delta dx$ in the stretched state makes no sense $x$ and $dx$ are defined for the unstretched state.

So what equation can you write for Δ(dx) in terms of dx and T?

$$Y = \frac{T dx}{A \Delta (dx)} $$

My original doubt was as to why only $T$ is producing longitudinal stress on dm and not the Tension acting in the upward direction shouldn't the equation be
$$Y = \frac{2T dx}{A \Delta (dx)} $$
as the tension acting in the upward direction is $T + dT$

 

[haruspex]

My original doubt was as to why only T is producing longitudinal stress on dm and not the Tension acting in the upward direction

That's a basic misunderstanding about tension and compression. As I posted, you should not think of these as forces in the ordinary way but as pairs of opposing forces. If I tie a rope to a wall and pull on it with force T then the tension is T all the way along, not 2T. Each element of the rope is subject to a force T in each direction, and we call that the tension.

 

[Hamiltonian]

That's a basic misunderstanding about tension and compression. As I posted, you should not think of these as forces in the ordinary way but as pairs of opposing forces. If I tie a rope to a wall and pull on it with force T then the tension is T all the way along, not 2T. Each element of the rope is subject to a force T in each direction, and we call that the tension.

ok, I think this makes sense thanks:)