Finding the Oscillations of Pendulum A

[happyparticle]

Homework Statement

Finding when the oscillations of the mass A will be at the minimum amplitude for the first time.

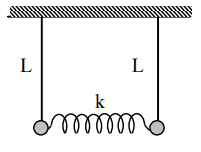
At t = 0, pendulum A = $x_a = 5cm$ and pendulum B = $x_a = 0$

Relevant Equations

normal modes coordinates
$q_p(t) = A cos \omega_p t$
$q_b(t) = B cos \omega_b t$

First of all, I found the angular frequencies for both pendulum and breathing mode which are
$\omega_p = 4.95$
$\omega_b = 7.45$

Then I found the normal mode coordinates equations:

$q_p(t) = A cos \omega_p t$
$q_b(t) = B cos \omega_b t$

And the beating frequency (I'm not sure if I need it or even if the value is correct)
$f_{beat} = 0.4$

Because the initial velocities are zero, the amplitude of each normal mode is equal to the initial value of the normal mode coordinate.
The pendulum A is at $x_a = 5$ and because the pendulum B is at $x_a = 0$ the initial position of the pendulum a (I guess)$q_p = x_1 + x_2, q_b = x_1 - x_2$
$q_p = 5 + ?, q_b = 5 - ?$

then

$q_p(t) = (5 + ?) cos \omega_p t$
$q_b(t) = (5-?) cos \omega_b t$

I know as well that
$x_1 = \frac{q_p(t) + q_b(t)}{2}$
$x_2 = \frac{q_p(t) - q_b(t)}{2}$

I'm stuck there. I still not sure about $x_2$ position and I can't see when the oscillations of the pendulum A will be at the minimum amplitude for the first time.

 

[haruspex]

Is this with the same diagram as in https://www.physicsforums.com/threads/coupled-oscillators-period-of-normal-modes.999869/?

 

[happyparticle]

Is this with the same diagram as in https://www.physicsforums.com/threads/coupled-oscillators-period-of-normal-modes.999869/?

Yes, sorry I forgot again.

 

[haruspex]

$q_p = 5 + ?, q_b = 5 - ?$

Why the signs and question marks? You have x₁(0)=5 and x₂(0)=0, no?
But you cannot assume the pure cosine formula for both. There may be a phase difference.

 

[happyparticle]

Why the signs and question marks? You have x₁(0)=5 and x₂(0)=0, no?
But you cannot assume the pure cosine formula for both. There may be a phase difference.

I'm not sure. because the statement say pendulum B at $x_a = 0$ so I guess it is not at the initial position. I think the initial position for the pendulum b is $x_b = 0$

 

[haruspex]

I'm not sure. because the statement say pendulum B at $x_a = 0$ so I guess it is not at the initial position. I think the initial position for the pendulum b is $x_b = 0$

Well I am rather confused by this statement:
"At t = 0, pendulum A = x_a=5cm and pendulum B = x_a=0."
I assume you meant "pendulum B = x_b=0." and that x₁ is the same as x_a, etc.
If that's not what x_a means, please explain.

 

[happyparticle]

I'm as confuse as you.
That's why the question marks.
However, it's really pendulum A at $x_a = 5 cm$ pendulum B at $x_a = 0$ So I suppose the pendulum B is at the initial position of pendulum A.

My guess is if the pendulum A moves from $x_a = 0$ to $x_a = 5cm$ and the pendulum B moves from $x_b = 0$# to $x_a = 0$ the pendulum b has also moved of 5cm. Finally it doesn't make sense. I don't have the distance between the pendulum A and B.Maybe pendulum B = pendulum A - 5cm

I assumed that A = $x_a = 5$ and B = $x_b = 0$

I get

$x_a(t) = \frac{5}{2}(cos \omega_p t + cos \omega_b t)$
$x_b(t) = \frac{5}{2}(cos \omega_p t - cos \omega_b t)$

However, what should be the next step to find the first time the pendulum A reach the minimal amplitude.

 

[haruspex]

it doesn't make sense. I don't have the distance between the pendulum A and B.
I get

$x_a(t) = \frac{5}{2}(cos \omega_p t + cos \omega_b t)$
$x_b(t) = \frac{5}{2}(cos \omega_p t - cos \omega_b t)$

However, what should be the next step to find the first time the pendulum A reach the minimal amplitude.

I don't think the distance between their rest points matters, as long as they don't collide! We are only concerned with the displacement of each from its rest point.

The puzzle is, what is meant by reaching a minimum amplitude?

We could write each displacement in 'beat' form, i.e. as a product of two trig functions, and take the higher frequency factor as the oscillation and the (magnitude of the) lower frequency factor as representing a varying amplitude. The first minimum would then be where that magnitude is first zero.

Alternatively, we could consider the instantaneous amplitude as only meaningful at a local extremum of displacement, i.e. whenever the velocity is zero. These points will form a time sequence, and the displacement magnitudes at these points will vary. A minimum amplitude would then be a local minimum in that sequence.

These two interpretations will probably not lead to the same answer.

I would go with the beat interpretation and see where it leads.

 

[happyparticle]

Do you mean something like
$x_a(t) = \frac{5}{2} cos (\frac{\omega_p + \omega_b}{2})t + cos (\frac{\omega_p - \omega_b}{2})t$

$cos (\frac{\omega_p - \omega_b}{2})t$ is the lower frequency factor

$cos (\frac{\omega_p - \omega_b}{2})t = 0$ when $\omega_p = \pi + \omega_b$

If I plug those values I still don't know $x_a(t)$ and of course t.

I'm wondering why the first minimum would be where that magnitude is first zero.

 

[haruspex]

Do you mean something like
$x_a(t) = \frac{5}{2} cos (\frac{\omega_p + \omega_b}{2})t + cos (\frac{\omega_p - \omega_b}{2})t$

$cos (\frac{\omega_p - \omega_b}{2})t$ is the lower frequency factor

No, factor, not one term in a sum. And you left out several parentheses.
You have to write $\frac{5}{2}( cos ((\frac{\omega_p + \omega_b}{2})t)+ cos ((\frac{\omega_p - \omega_b}{2})t))$ as a product of two trig functions, not as a sum.

 

[happyparticle]

I made a mistake
$x_a(t) = \frac{5}{2} cos (\frac{\omega_p + \omega_b}{2})t cos (\frac{\omega_p - \omega_b}{2})t$

 

[anuttarasammyak]

As a general approach we may make Lagrangean of the system
$$L=T-V$$
$$T=\frac{1}{2}m_1l^2_1 \dot{\theta_1}^2+\frac{1}{2}m_2l^2_1 \dot{\theta_2}^2$$
$$V=-g[m_1l_1 \cos\theta_1+m_2l_2 \cos\theta_2]+\frac{k}{2}d^2$$
where
$$d=\sqrt{(l_1\cos\theta_1-l_2 \cos\theta_2)^2+(l_1\sin\theta_1-l_2 \sin\theta_2-R)^2}-l_0$$
R is distance between the pendulum supports, $l_0$ is natural length of spring.
Applying Lagrange equation with some initial condition we get $\theta_1(t),\theta_2(t)$.

I do not catch intention of the problem but it may be better to introduce
$$\phi_1=\frac{\theta_1+\theta_2}{2}$$
$$\phi_2=\frac{\theta_1-\theta_2}{2}$$
to get $L(\phi_1,\phi_2,\dot{\phi_1},\dot{\phi_2})$ for considering it.

 

[haruspex]

I made a mistake
$x_a(t) = \frac{5}{2} cos (\frac{\omega_p + \omega_b}{2})t cos (\frac{\omega_p - \omega_b}{2})t$

Ok, but that makes it look as though the time variable is outside the trig function.
Clearer as $x_a(t) = \frac{5}{2} \cos ((\frac{\omega_p + \omega_b}{2})t) \cos ((\frac{\omega_p - \omega_b}{2})t)$.
(In LaTeX you can put a backslash in front of standard functions, like cos, ln, to stop them being italicised.)
So which of those two factors do you consider to represent a varying amplitude, and when is it first zero?

 

[happyparticle]

$\cos(\frac{\omega_p-\omega_b}{2}t)$ represent a varying amplitude.

it is first zero when $\frac{\omega_p-\omega_b}{2}t = \frac{\pi}{2}$

So when $t = \frac{\pi}{\omega_p - \omega_b}$

Then I plug the value of t to find $x_a(t)$ ?

 

[haruspex]

$\cos(\frac{\omega_p-\omega_b}{2}t)$ represent a varying amplitude.

it is first zero when $\frac{\omega_p-\omega_b}{2}t = \frac{\pi}{2}$

So when $t = \frac{\pi}{\omega_p - \omega_b}$

Looks ok to me. Presumably they want a numeric answer, though.

Then I plug the value of t to find xa(t) ?

Why? You know that will give 0. You are asked to find the time, which you have done.

 

[happyparticle]

So that's it ? I mean, I'm not sure to understand why when this factor is zero, the amplitude of the oscillations is at minimum.

 

[haruspex]

So that's it ? I mean, I'm not sure to understand why when this factor is zero, the amplitude of the oscillations is at minimum.

I would find it more convincing if the two modal frequencies were closer together, differing by no more than 15%, say. Then, plotting out the displacement of A would reveal a beat, and it would be reasonable to interpret the frequency difference as an amplitude modulation of an oscillation at the frequency sum.
But here your two frequencies are in a ratio 3:2. Still, that does put the sum and difference in the ratio 5:1, so I suppose it is just ok.
Plot it and see what it looks like.