Finding the output V of a filter

[Bolter]

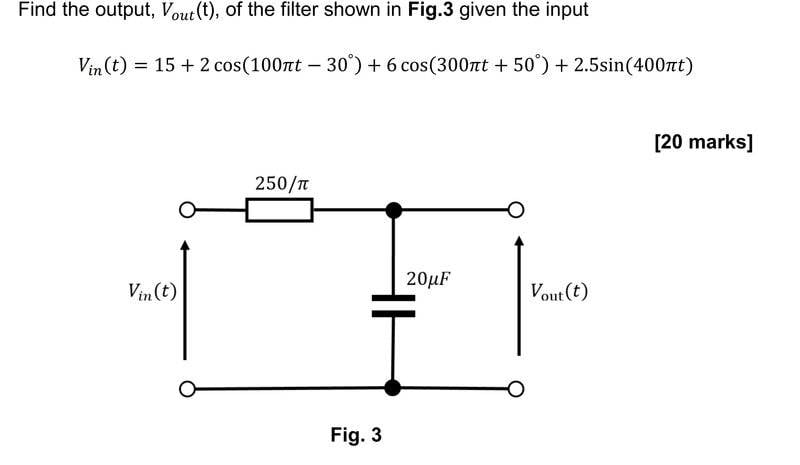
Homework Statement

To calculate the output V of a filter given the Vin equation

Relevant Equations

See image below

Hi everyone, I've been having trouble on how to answer this question

This is my attempt at it below, but I am not sure what values of t to sub in for evaluating the integral.

Any help would be appreciated! Thanks

 

[ergospherical]

Looks fine as is, the integrator output should be a function of time.

 

[Bolter]

Looks fine as is, the integrator output should be a function of time.

ok thanks, I was thinking there would be a set value at the end as the end result so it threw me off to begin with.

 

[DaveE]

I would reconsider your 1st line, the differential equation. Suppose you input a positive constant voltage $V_i$, your equation says that the output will fall at a constant rate forever $V_o =-(\frac{V_i}{RC})⋅t$. Does that seem correct?

You know that $v_o = \frac{1}{C} \int{i }{dt}$ , or $i = C\frac{dv_o}{dt}$ from the capacitor equation. where $i$ is the capacitor current. How does the current depend on the other variables?

 

[ergospherical]

The negative sign ought not really be there, but the dependence $V_{\mathrm{o}}(t) \propto t$ is expected for an integrator with constant input, no?

 

[Steve4Physics]

I’m no electronics expert so will be happy to be corrected. But I think there is a problem…

There is a DC component of 15 (presumably volts) as part of $V_{in}$. Treating the circuit as a simple integrator means that the output voltage is 15t (+ oscillatory components of constant amplitude). So the mean value of $V_{out}$ will grow indefinitely large – which doesn’t make sense.

Treating the circuit as an integrator is (I believe) only an approximation valid for oscillatory inputs where $\omega_{in} \gg \frac {1}{RC}$, So this excludes DC input.

Also, assuming the given value for resistance of 250/π is in ohms, then $\frac {1}{RC}$ = 628s⁻¹. The angular input frequencies (100π, 300π and 400π) are not much larger than $\frac {1}{RC}$. So we can’t even treat the circuit as an integrator for the AC components of $V_{in}$.

 

[ergospherical]

Oh yes, that's a good point, for a low frequency input you'd instead expect the $1- e^{-t/\tau}$ charging behaviour.

 

[Bolter]

So I'm I wrong to assume my equation in the first line to be incorrect?
This is how I reached to that equation

 

[DaveE]

Where does $i$ flow? How can you describe $i$ based on the circuit voltages?

Suppose at some instant in time we had $v_i = 5V$ and $v_o = 1V$, what would the capacitor current be? Now suppose at another instant in time we had $v_i = 6V$ and $v_o = 4V$, what would the capacitor current be?

 

[DaveE]

The negative sign ought not really be there, but the dependence $V_{\mathrm{o}}(t) \propto t$ is expected for an integrator with constant input, no?

It's not an integrator, it's a 1st order D.E.

 

[DaveE]

Also, mind the polarities when you make the KVL equations. Redraw the schematic and label everything you use in your equations, including their polarities.

 

[ergospherical]

It's not an integrator, it's a 1st order D.E.

I'm pretty sure it is an integrator, albeit approximate. Conserving current at the node between the resistor and capacitor implies\begin{align*}
\dfrac{V_{\mathrm{i}} - V_{\mathrm{o}}}{R} = C \dfrac{dV_{\mathrm{o}}}{dt}
\end{align*}Under the assumption that $V_{\mathrm{o}} \ll V_{\mathrm{i}}$, or equivalently $V_{\mathrm{i}} - V_{\mathrm{o}} \approx V_{\mathrm{i}}$, then you do indeed obtain $V_{\mathrm{o}} \approx \frac{1}{RC}\int_0^t V_{\mathrm{i}}(t') dt'$.

If the capacitor becomes sufficiently charged then the assumption that $V_{\mathrm{o}} \ll V_{\mathrm{i}}$ would fail to hold and the circuit would no longer act as an integrator (i.e. which would happen if you hold $V_{\mathrm{i}} = \mathrm{constant}$).

But for a high-frequency signal centered on $V_{\mathrm{i}} = 15 \ \mathrm{V}$, the output voltage ought to remain small and the integrator approximation justified.

 

[Bolter]

If I take it as a differentiator instead since its a first order differential eqn, then I get this as my new expression for V_out

Does this seem about right or not?

Sorry if the image is a bit hazy

 

[DaveE]

If I take it as a differentiator instead since its a first order differential eqn, then I get this as my new expression for V_out

View attachment 294559
Does this seem about right or not?

Sorry if the image is a bit hazy

No. Make two equations for the voltages around the loop based on the current. One equation is due to the capacitor, the other is due to the resistor. Use KVL to sum those voltages.

You are skipping steps and guessing. Be methodical. What is each voltage? each current? what equations relate them to each other?

 

[DaveE]

I'm pretty sure it is an integrator, albeit approximate... Under the assumption that $V_{\mathrm{o}} \ll V_{\mathrm{i}}$.

Nope. It is a circuit that behaves like an integrator in some circumstances.

I know, it's annoying and pedantic. But, this is exactly the problem the OP is having understanding this circuit. Once you've simplified a circuit to such a basic level, approximations aren't the point anymore. In that exponential step response, the boring parts are the linear part near 0 and the flat part near infinity. This sort of question is all about the curvy bits in the middle.

BTW, you will find in simple passive linear circuits, you will never see a true integrator that isn't turning voltage into current or vice-versa. Voltage in - voltage out integrators don't work in the passive world.

 

[ergospherical]

I don't know how to solve for the exact solution of the differential equation for the given function $V_{\mathrm{i}}(t)$ in the problem statement, so making the approximation $V_{\mathrm{o}} \ll V_{\mathrm{i}}$ seems to me like the only way one could be expected to do it. Do you have another approach in mind?

 

[BvU]

It's not an integrator, it's a 1st order D.E.

I fully agree. So I am a little surprised the problem statement does not give an initial condition. It also wrongfoots people using the term "filter".

linear circuits

An important clue ! The input is a sum of four terms. After a while (a settling time, a number of RC times) it is possible to consider the output as the sum of the four responses. To me it is unclear if the exercise composer is searching such an answer (the term "filter" suggests so, but we don't know the context). If the desired answer is a complete expression $V_o(t)$ from t=0 onwards I find the exercise badly composed.

$\$

 

[DaveE]

I don't know how to solve for the exact solution of the differential equation for the given function $V_{\mathrm{i}}(t)$ in the problem statement, so making the approximation $V_{\mathrm{o}} \ll V_{\mathrm{i}}$ seems to me like the only way one could be expected to do it. Do you have another approach in mind?

I fully agree. So I am a little surprised the problem statement does not give an initial condition. It also wrongfoots people using the term "filter".

Yes, we EEs are so used to these linear DEs that we usually ignore or give short shrift to the "exact solution". The catechism is to solve for the transfer function (impulse response, etc.) and just assume that y'all will do the convolution or Laplace solution for your scenario. It's a consequence of the benign nature of linear systems (superposition et.al.). Once you know the dynamics, the rest is a) boring, and b) application specific. This is especially true for initial conditions, but also applies to driving functions. Nearly always it's either a computation your computer does, or it's something really simple like a step, ramp, or sine wave. In the real world of analog EE, frequency response is king and you get a spectrum analyzer or do a Fourier transform to apply that to your waveform.

For a problem like this, we would just use phasors and find the gain and phase shift at those specific frequencies (because, superposition). It's rare that we actually have to solve the DEs. We would immediately jump to the Laplace "space" and stay there. We also would separate the steady state solution from the transients and probably ignore one or the other.

This can be a real problem when you're teaching, because we aren't even aware of the assumptions that we always make but that you don't know about yet. Things like what does "filter" mean?

 

[DaveE]

So I'm I wrong to assume my equation in the first line to be incorrect?
This is how I reached to that equation

View attachment 294558

If you've studied phasors (complex impedance, etc.), that is another, perhaps easier, way to approach this problem. i.e. what is the gain and phase shift at each of those input frequencies? If you haven't, don't worry about it, it's not a necessary approach.

 

[DaveE]

If the desired answer is a complete expression Vo(t) from t=0 onwards I find the exercise badly composed.

On the one hand, they usually are.

But, this one isn't too bad for HW problems. Since there is no reference to any transient inputs, there is no discussion of what happens at/before t=0, and there is no time dependent question like when does something happen, or what is some value at t=t_o. It would be normal to assume that they are only asking about the steady state solution. In which case the ICs are irrelevant, they will decay to zero (except pathologic cases, like negative resistors and such).