Finding the position of a middle charge to have Zero Net Force

[sylent33]

Homework Statement

Find the new position of Q3

Relevant Equations

Coloumbs Force

Hi!

Given three voltages as follows;

Q1 = 1C,Q2 = 1C,Q3 = 2C

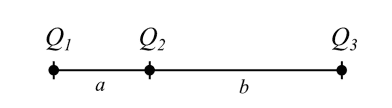
The distance a is 1m and b = 2m

a) Find the values of the forces that are acting on Q2

I did that like this;

$$ F_{12} = \frac{Q1*Q2}{4\pi\epsilon r^2} $$
$$ F_{32} = \frac{Q1*Q3}{4\pi\epsilon r^2} $$

The results are : $F_{12} = 8,99 GN and F_{13} = 4,49 GN$

b) What is the direction and value of the total force as a sum of the individual forces. Here was also given a hint as follows:

"Think in terms of vectors"

My idea here was this: The force F12 is moving from Q1 to Q2,so its moving from left to right,the force F32 is moving from Q3 to Q2.Now they are going against each other,that would mean,in terms of vectors that I would have to subtract them from each other.Hence;

$F_{total} = 4,5 GN$ For the direction of Ftotal I am not sure.I think it should be from left to right since the force acting from the left (F12) is much greater (2x almost) than the force from the right (F32) so that would mean that it will "push out" and that Fg is poining to the right.

c) How would you need to chose a so that no force acts upon Q2

In order to be no force onto Q2 all the forces acting upon it have to be zero,hence;

$$ F_{12}+F{32} = 0 $$

$$ F_{12} = \frac{Q1*Q2}{4\pi\epsilon a^2} + F_{32} = \frac{Q2*Q3}{4\pi\epsilon r^2} = 0$$

since we want a,we need to move F32 to the other side.Than do some simplification;
$$ \frac{Q2}{a^2} = -\frac{Q3}{ r^2} $$

Plug in values

$$ \frac{1}{a^2} = -\frac{2}{ 2^2} $$

Solve for a

$$ a = \sqrt{-2} $$

And obviously this is not correct. The solution says it should be 1,41m which is just sqrt of 2.I am not sure how they get there,I've checked my algebra multiple times and it looks correct.It only leaves my initial idea to be at fault which is where I need a bit of help. How would you approach the problem c)?

Also what do you think about my solution/thought process in b) ?

Many thanks and greetings!

 

[Gordianus]

Check the line where you add forces. Remember they're vectors.

 

[sylent33]

Check the line where you add forces. Remember they're vectors.

Hi,
I assume you are referring to the c) task and to my statement
F12 + F32 = 0 ?
I am not sure what exactly you mean with "remember they are vectors" ? Are you implying that I should add them like I would 2 vectors? X component with X Y with Y etc?

 

[Gordianus]

The idea that $$\vec F_{12}+\vec F_{32}=\vec 0$$ is correct. However, you considered ONLY the moduli.

 

[BvU]

Furthermore: you let $F_{32}$ depend on $Q_1$ -- you may want to check that

$\$

 

[sylent33]

Oh I think I get it now. I need to take into account the direction of the vectors. Now simply using the fact that I need F32 to be negative for my equation to work out I can say F12 - F32 = 0 and than it would all work.

But how would/should I determine the direction generally?

Also as Bvu pointed out I have an typo in F32 it should be Q2*Q3 but still it does not matter since the values for Q1 and Q2 are the same. I will edit it out.

 

[Gordianus]

$$\vec F_{mn}=\frac{1}{4\pi \varepsilon_{0}} Q_mQ_n \frac{(\vec r_m-\vec r_n)}{|\vec r_m-\vec r_n|^3}$$
This is the vector formula for the force on charge "m" due to the interaction with charge "n"

 

[sylent33]

$$\vec F_{mn}=\frac{1}{4\pi \varepsilon_{0}} Q_mQ_n \frac{(\vec r_m-\vec r_n)}{|\vec r_m-\vec r_n|^3}$$
This is the vector formula for the force on charge "m" due to the interaction with charge "n"

After working with this formula I get to the right equation. But I was wondering if I could have simply gone off the fact and said;

F12 is pointing right so its positive,F32 is pointing left so its negative? And just set up the equation like that

Thanks!

 

[BvU]

Yes you could. This is a simple configuration. Once it gets more complicated (e.g. a continuous charge distribution somewhere), you will need the general form. So it is worth the investment to get familiar with it.

Note also that your $F_{mn}$ notation is the opposite of that in the expression posted by @Gordianus and many others. Check your textbook and stick to that !

$\$

 

[sylent33]

Yes you could. This is a simple configuration. Once it gets more complicated (e.g. a continuous charge distribution somewhere), you will need the general form. So it is worth the investment to get familiar with it.

Note also that your $F_{mn}$ notation is the opposite of that in the expression posted by @Gordianus and many others. Check your textbook and stick to that !

$\$

Oh,so I overcomplicated as per usual. And that about the notation is confusing but in our notations its how i proposed; if Q1 is acting on Q2 than it is F12. I am sticking to that.

Thanks for the help!