Finding the position vector for translated frame of reference

[simphys]

Homework Statement

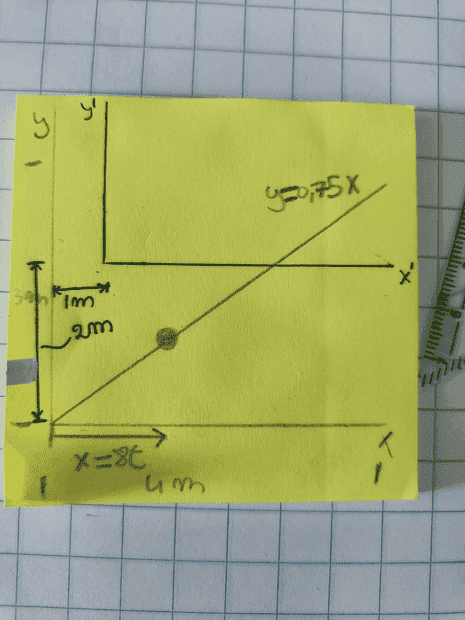
Please refer to the picture, I don't really have a question problem.
I was posed the question on how I would model what the position would be when the frame of reference is translated as shown on the picture.

Relevant Equations

$\vec r = 8t \hat i + 6t \hat j$ for the y-x reference framse.

what would be the y'-x' $\vec r$ vector be?

I think it is
$\vec r = (8t - 1) \hat i + (6t - 2) \hat j$ (not sure whether it is correct or not.)
I thought about it as at t = 0 the position needs to be -1i -2j so that is why I took the signs in the y'-x' frame position vector as a - instead of + signs for 1 and 2.

Is it ok to reason like this or do I need to derive it from somewhere else? I am not very acquianted with translation of the axes that's why I am asking.
Thanks in advance.

 

[malawi_glenn]

What is the origin of x' y' system as measured in the x y system?

 

[simphys]

What is the origin of x' y' system as measured in the x y system?

in points (1,2) = (x,y)

 

[malawi_glenn]

can you find a relation for the vectors $\vec R$, $\vec r$ and $\vec r\:'$?

 

[simphys]

What is the origin of x' y' system as measured in the x y system?

oh wait, isn't this actually the 'relative frames of references' that are used to describe relative motion?
than it becomes r_x/p = r_x'/x + r_p/x' (where the condition was that it should be an inertial frame aka cst velocity or at rest for it to be valid)

 

[simphys]

View attachment 304325
can you find a relation for the vectors $\vec R$, $\vec r$ and $\vec r\:'$?

yep exactly my post #5 no?

 

[simphys]

Thanks a lot @drmalawi, appreciate it!

 

[malawi_glenn]

aka cst

?

 

[simphys]

?

constant, apologies.

 

[malawi_glenn]

constant, apologies.

np glhf