Finding the possible Resistances in order to Critically Damp a Circuit?

[luap]

Homework Statement

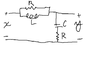
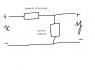
In the circuit given below, specify values for R such that the system is critically damped. Let L =2 Henry, and C= 0.01 farads.

Homework Equations

1 = $$\alpha$$ / $$\omega$$

The Attempt at a Solution

I don't know really where to begin. The next question asks us to find the transfer function with the Larger value of R, so I'm assuming there are 2 solutions in which R can be. Anything that could help my brain go in the right direction would be much appreciated! I attached a picture I drew of the circuit.

 

[vela]

Start by finding the transfer function for that circuit.

 

[luap]

Alright I went ahead and did my best to find the transfer function in terms of R and s, but my final answer doesn't make much sense to me.

I just used the s domain and transformed the circuit into a simple voltage divider. I transformed the parallel RL portion to
$$\frac{R*2s}{R+2s}$$

then I added the series RC into
$$\frac{100}{s} + R$$

Then solved the voltage for y by using a voltage divider (note the attachment). I did some simplifying and came up with this transfer function. Which makes no sense to me.
$$\frac{y}{x}=H=\frac{2R(s^2) + 200s + (R^2)*s + 100R}{4R(s^2) + 200s + (R^2)*s + 100R}$$

 

[vela]

It might help if you didn't plug the numbers in right from the beginning. In symbols, you'd get

$$H(s) = \frac{(Ls+R)(RCs+1)}{2RLCs^2+(R^2C+L)s+R} = \frac{1}{2}\left[\frac{(s+\frac{R}{L})(s+\frac{1}{RC})}{s^2+\frac{1}{2}(\frac{R}{L}+\frac{1}{RC})s+\frac{1}{2LC}}\right]$$

The combinations like R/L, 1/RC, and 1/LC should look familiar to you. The denominator of H(s) corresponds to the differential equation the oscillator satisfies. Each factor of s indicates a differentiation, so the differential equation would be

$$y''+\frac{1}{2}\left(\frac{R}{L}+\frac{1}{RC}\right)y'+\left(\frac{1}{2LC}\right)y=f(t)$$

Compare that to the general differential equation for a damped harmonic oscillator to figure out when the circuit will be critically damped.

 

[DeeNos]

To find the possible resistances for critical damping in this circuit, we can use the formula for the damping ratio, which is given by:

ζ = R/2√(L/C)

For critical damping, the damping ratio should equal 1. So, we can set ζ = 1 and solve for R:

1 = R/2√(L/C)

R = 2√(L/C)

Substituting the given values of L = 2 Henry and C = 0.01 farads, we get:

R = 2√(2/0.01) = 200 Ω

So, for critical damping in this circuit, the resistance should be 200 Ω. This is the only possible value of R for critical damping in this specific circuit.