Glenn G
- 113
- 12
Thread moved from the technical forums to the schoolwork forums
TL;DR Summary: Finding the power loss in a wire of varying area - my problem is I don't know how to set up the integral
Hopefully you can see in the diagram below that the area of the wire varies linearly with length. I know the equations for resistance and power loss and I can express the resistance of a thin slice but need to integrate over the whole wire to get the full resistance - to find power then it is trivial. I've thought about this for a good while now but can't get it. Please help, this isn't homework (I'm very old and doing this for fun!)
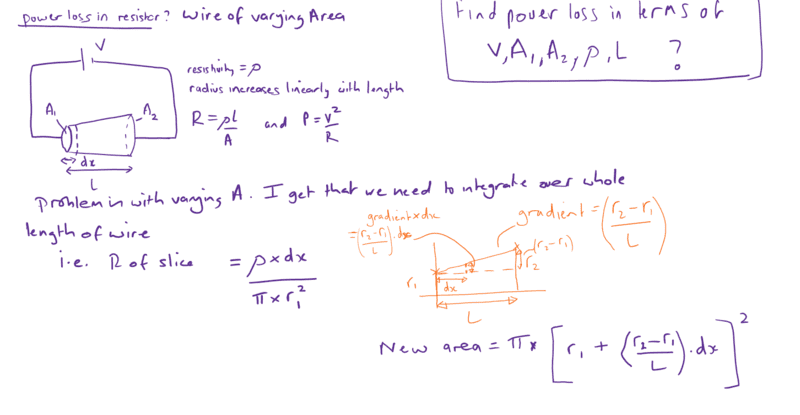
Hopefully you can see in the diagram below that the area of the wire varies linearly with length. I know the equations for resistance and power loss and I can express the resistance of a thin slice but need to integrate over the whole wire to get the full resistance - to find power then it is trivial. I've thought about this for a good while now but can't get it. Please help, this isn't homework (I'm very old and doing this for fun!)