Amaelle
- 309
- 54
- Homework Statement
- Loook at the image
- Relevant Equations
- Power series.
Raduis of convergence.
Greetings
I have some problems finding the correct result
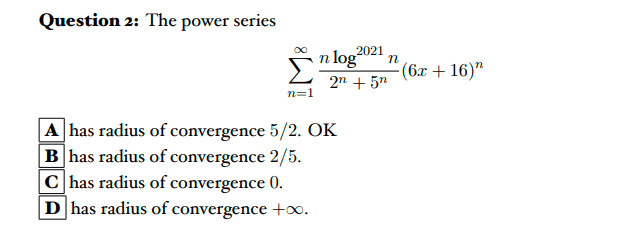
My solution:
I puted Y=6x+16
so now will try to find the raduis of convergence of Y
so let's calculate the raduis criteria of convergence:




I would like to know where is my mistake
thank you!
I have some problems finding the correct result
My solution:
I puted Y=6x+16
so now will try to find the raduis of convergence of Y
so let's calculate the raduis criteria of convergence:
- We know that Y=6x+16
- Conseqyently -21/6<=x<=-11/6 so the raduis must be 5/3. But this is not the solution!
I would like to know where is my mistake
thank you!