Finding the radius of the sphere

[kaspis245]

Homework Statement

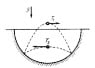
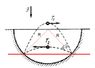
In a spherical bowl a small ball is jumping around. The ball hits the bowl in two spots and moves in two different trajectories in times T₁, T₂. Find the radius of the bowl.

Homework Equations

Newton's laws of dynamics.

The Attempt at a Solution

The only thing I could figure out is how the horizontal velocities of different trajectories are related:
s=v_{x1}⋅T_1=v_{x2}⋅T_2 ⇒ \frac{v_{x1}}{v_{x2}} = \frac{T_2}{T_1}
But I can't find a way to get any expression with the radius. Please help.

 

[mfb]

What do you know about the incoming and outgoing angle for a perfectly elastic collision?

Unrelated to that: You will probably need the trajectories in both parts.

 

[kaspis245]

What do you know about the incoming and outgoing angle for a perfectly elastic collision?

Momentum is conserved. Then the velocities of both trajectories are equal. I still can't see how the radius is related to any of this.

 

[ehild]

Momentum is conserved. Then the velocities of both trajectories are equal. I still can't see how the radius is related to any of this.

The ball interacts with the bowl which is much bigger than the ball. You can consider the bowl of infinite mass. The velocities are not the same, but energy might be conserved. What would it mean for the speeds?
The ball performs two different projectile motions with the same range.

 

[BvU]

$$
s=v_{x1}⋅T_1=v_{x2}⋅T_2 ⇒ \frac{v_{x1}}{v_{x2}} = \frac{T_2}{T_1}$$

Are you saying the two different trajectories have the same path length ?

 

[kaspis245]

Ok, so the velocities are not equal. I can’t really apply the momentum conservation law since the direction of motion changes after the impact, and I don’t have any angles.

As for the energy I can only say that v_1<v_2 since the path T_1 has more potential energy (jumps higher).

Are you saying the two different trajectories have the same path length ?

The trajectories have the same horizontal distance, which I denoted by s.

 

[ehild]

Ok, so the velocities are not equal. I can’t really apply the momentum conservation law since the direction of motion changes after the impact, and I don’t have any angles.

As for the energy I can only say that v_1<v_2 since the path T_1 has more potential energy (jumps higher).

What do you mean on v₁ and v₂?
The problem said

In a spherical bowl a small ball is jumping around.

that means the ball repeats its motion, so the collisions can be considered elastic.
The ball has both horizontal and vertical components of velocity. It jumps higher if the vertical component is bigger.
T₁ and T₂ are the times between two collisions with the bowl.

 

[BvU]

Ok, so the velocities are not equal

It's the directions, and the directions only, that change !