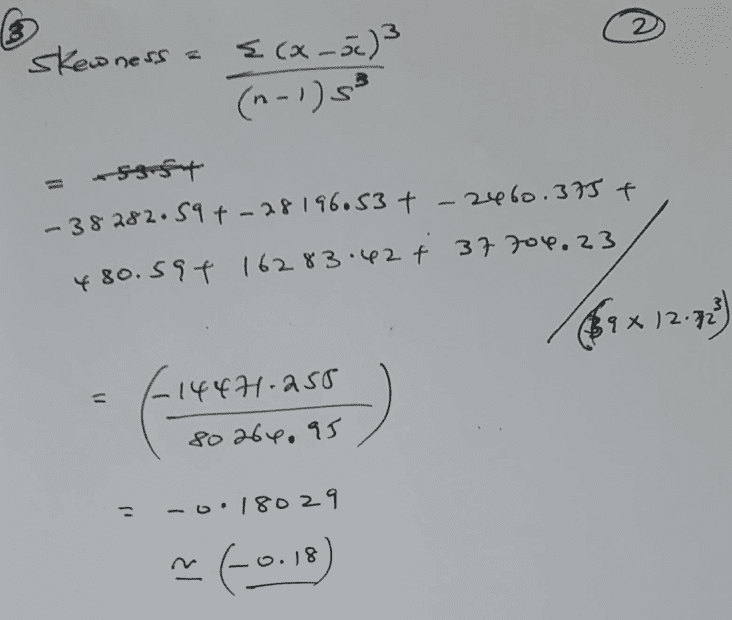- #1
chwala
Gold Member
- 2,753
- 388
- Homework Statement
- See attached below
Note that this is an original problem created by myself.
- Relevant Equations
- Skewness and kurtosis- Statistics
See the grouped data below; I just want to be certain that i have followed the correct step in trying to find skewness of the grouped data.