Finding the solution to system of 3 equations with 3 unknowns

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this,

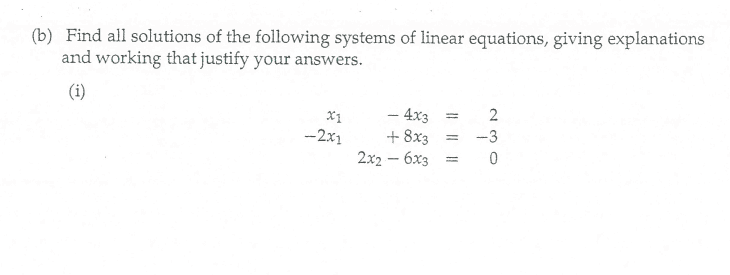
I am trying to find solutions, however, I think I am getting a strange result that I am not too sure how to intercept.

I first multiply the first equation by 2 to get $2x_1 - 8x_3 = 4$ and then I add it to the second equation below to get $0 = 1$. I think this means that there is no values for $x_1$ or $x_3$ that satisfy the equation. I am not too sure how to go from here but I know $x_2$ is a leading variable of the third equation.

Any help is greatly appreciated

Many thanks!

 

[fresh_42]

I first multiply the first equation by 2 to get $2x_1 - 8x_3 = 4$ and then I add it to the second equation below to get $0 = 1$. I think this means that there is no values for $x_1$ or $x_3$ that satisfy the equation.

Right. If you multiply the first line by $-2$ then you get $-2x_1+8x_3= -4$ and $-2x_1+8x_3= -3.$
This cannot hold at the same time.

I am not too sure how to go from here but I know $x_2$ is a leading variable of the third equation.

Any help is greatly appreciated

Many thanks!

The solution space is empty. There is nothing left that can be done.

 

[FactChecker]

get $0 = 1$. I think this means that there is no values for $x_1$ or $x_3$ that satisfy the equation. I am not too sure how to go from here

Good work. Sometimes the hardest problems are the ones that give you an unexpected result. Just double-check your result and accept what it says. Your result is not just about $x_1$ and $x_3$, it is about $0 \ne 1$. So nothing more can be done.