Finding the speed of the block for one and two springs

[miyayeah]

Homework Statement

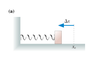
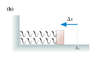
The spring in the figure (Figure 1) is compressed by length Δx. It launches the block across a frictionless surface with speed v0. The two springs in the figure (Figure 2) are identical to the spring of figure 1. They are compressed by the same length Δx and used to launch the same block. What is the block's speed now (for figure 2)?

Figure 1:

Figure 2:

Homework Equations

Ui = Kf
Esp = ½ k ⋅ Δx²
Esp = K = ½ mv²
(as it launches off)

The Attempt at a Solution

I am not sure how having double the spring would affect the block's speed. I assumed it would increase (double) the spring potential energy because two of the same spring from Figure 1 are present for the situation in Figure 2. Would the speed for Figure 2, then, be simply 2V0?

v/v0 is also in front of the answer box, and I am not sure why.

Any help would be much appreciated!

 

[kuruman]

Is the potential energy doubled?
Is the kinetic energy doubled?
If the answer to both questions above is "yes", is the speed doubled?

Write a few equations down.

 

[TSny]

Hello

The Attempt at a Solution

I am not sure how having double the spring would affect the block's speed. I assumed it would increase (double) the spring potential energy because two of the same spring from Figure 1 are present for the situation in Figure 2.

Yes, that's right.

Would the speed for Figure 2, then, be simply 2V0?

Why would that be? Hint: Think about how the final kinetic energies of the two cases compare.

v/v0 is also in front of the answer box, and I am not sure why.

Maybe they are asking you to give the ratio of the velocity with two springs to the velocity with one spring. So, the answer will just be a number with no units.

 

[miyayeah]

Is the potential energy doubled?
Is the kinetic energy doubled?
If the answer to both questions above is "yes", is the speed doubled?

Write a few equations down.

Hello
Yes, that's right.

Why would that be? Hint: Think about how the final kinetic energies of the two cases compare.

Maybe they are asking you to give the ratio of the velocity with two springs to the velocity with one spring. So, the answer will just be a number with no units.

½ k ⋅ Δx² = ½ mv²

When potential energy is doubled, k ⋅ Δx² = mv², so
v= √[(k ⋅ Δx²)/m]

This is the same velocity as when there is only one spring. So would the speed for both situation be the same?

 

[kuruman]

U₁=K₁
U₂=K₂
You have U₂=2U₁ because you have two springs compressed by the same amount Δx. OK so far.
Now an expression for K₁ is ½mv₁². What do you think should be an analogous expression for K₂?

 

[miyayeah]

U₁=K₁
U₂=K₂
You have U₂=2U₁ because you have two springs compressed by the same amount Δx. OK so far.
Now an expression for K₁ is ½mv₁². What do you think should be an analogous expression for K₂?

That helped a lot, I realized I have to use some kind of formula for that relationship between the two situations. I was able to get the answer to the question.
Thank you!