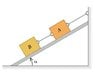
- #1
Yosty22
- 185
- 4
Homework Statement
Two blocks, each with weight ω, are held in place by a frictionless incline.
In terms of ω and the angle θ of the incline, calculate the tension of the rope connecting the two blocks.
Homework Equations
ƩF=ma
The Attempt at a Solution
Since it is on a tilted incline, with angle θ, I made the x and y-axis tilted for the free body diagram. This means that ω, the weight, can be broken down into components ωx, which is parallel to the tension, and ωy, perpendicular to tension. In this case, I assumed that all forces acting in the x-direction (parallel to the tension) were ωx and T. I then used the equation ƩF=max and plugged in values and solved for T. First, I put "ωsinθ" in place of ωx, making the equation ωsinθ+T=ma. Solving for T, I get T=ma-ωsinθ. Is this correct? It looks a little odd to me.