Undergrad Finding the vibrational partition function of a diatomic molecule

[thegirl]

Hi,
How did they break down the following summation?

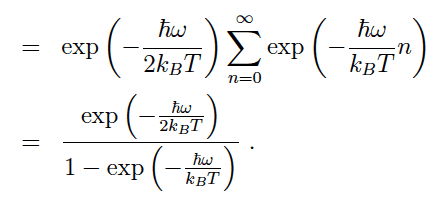
When finding the vibrational partition function ofa diatomic molecule it was approximated that the energy levels of the vibrational part of the diatomic molecule were harmonic and therefore the energy equation for a harmonic oscillator was used. Is the summation made to equal (1 - exp( - hw/KbT))^-1 because there are two degrees of vibrational freedom and therefore two energy levels? Or isit just due to maths?

 

[DrClaude]

It's just the math:
$$
\sum_{n=0}^{\infty} x^n = \frac{1}{1 -x}
$$
for $|x|<1$.

 

[thegirl]

Omg, thank you!