Finding the volume of these figures

[yik-boh]

Homework Statement

Find the volume of the described figures

1. A pyramid with height h and base an equilateral triangle with side a (a tetrahedron).

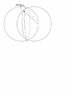
2. Find the volume common to two spheres each with radius r, if the center of each sphere lies on the surface of the other sphere.

These are hard problems and I really do not know what to do. Our teacher gave this to us as a challenge and I really would like to know how to solve these two. I hope you can help me by explaining each important step you will take. I hope you can make it detailed as much as possible. I really am having a hard time in Calculus. Thanks! :)

 

[CompuChip]

For 1): you can slice the tetrahedron horizontally into pieces of height dz. Then each piece will again be an equilateral triangle whose sides decrease from a at z = 0 to 0 at z = h.

For 2): you can slice the intersection of the spheres into circles of thickness d\theta whose radius r(\theta) increases from r(\theta = -\pi / 2) = 0 to r(\theta = 0) = r (see attachment) and you can use some fancy trig work to find the expression for r(theta).

 

[HallsofIvy]

It was you the teacher was challenging, not us! There are a number of different ways to do these problems ranging from looking up standard formulas to using Calculus as CompuChip suggests.

 

[yik-boh]

For 1): you can slice the tetrahedron horizontally into pieces of height dz. Then each piece will again be an equilateral triangle whose sides decrease from a at z = 0 to 0 at z = h.

For 2): you can slice the intersection of the spheres into circles of thickness d\theta whose radius r(\theta) increases from r(\theta = -\pi / 2) = 0 to r(\theta = 0) = r (see attachment) and you can use some fancy trig work to find the expression for r(theta).

I'm sorry but I don't exactly get it. I'm really having a hard time in Calculus right now.

For #1, what is dz? Just a representation for height? and I can't picture properly the tetrahedron I need to slice.

For #2, I really don't get it. I'm sorry.

I hope you'll still explain it to me.

 

[yik-boh]

I got the 1st one already. Only #2 left.

 

[CompuChip]

Here is another hint, hopefully it clarifies a bit better what I meant.
The volume of the little circular disc (actually, it's a cylinder with radius r and thickness dtheta) that I drew is \pi r^2 \, d\theta. Of course you'll have to express r as a function of theta before you do the integration (and find the appropriate limits for theta).