Finding vectors parallel to a given vector

[member 731016]

Homework Statement

Please see below

Relevant Equations

Coordinate form of vector

For (b) of this problem,

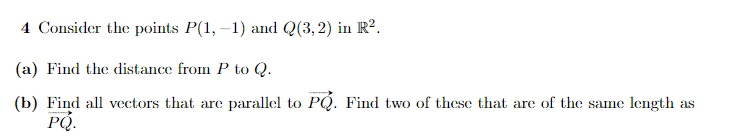
The solution is,

However, I am confused why the two parallel vectors are $(\frac{2}{\sqrt{13}}, \frac{3}{\sqrt{13}})$ and $(-\frac{2}{\sqrt{13}}, -\frac{3}{\sqrt{13}})$ should it not be $(2,3)$ and $(-2,-3)$. Do somebody please know why they wrote that?

Also I am very confused with this notation

Many thanks!

 

[FactChecker]

You are correct. The length of $\overrightarrow {PQ}$ is $\sqrt {13}$, so they gave a unit vector as the answer. Their notation appears to mean the unit vector in that direction. That is not what the problem asked for.

 

[Mark44]

However, I am confused why the two parallel vectors are $(\frac{2}{\sqrt{13}}, \frac{3}{\sqrt{13}})$ and $(-\frac{2}{\sqrt{13}}, -\frac{3}{\sqrt{13}})$ should it not be $(2,3)$ and $(-2,-3)$. Do somebody please know why they wrote that?

Did the published answer to the question give $(\frac{2}{\sqrt{13}}$ and $\frac{3}{\sqrt{13}})$ as the answers? If so, these answers are wrong as they did not ask for the vectors to be unit vectors.

The other thing you asked about, PQ with both an arrow above it and a caret (or hat, for a unit vector), is unusual notation, in my experience. Usually, one or the other is used, but not both.

 

[pasmith]

The only vectors which are parallel to a given vector and which are of the same length as that vector are that vector itself and its negative.

 

[FactChecker]

I wonder if the answer was cut off and the unit vectors were multiplied in the final step that is not shown?

 

[member 731016]

Did the published answer to the question give $(\frac{2}{\sqrt{13}}$ and $\frac{3}{\sqrt{13}})$ as the answers? If so, these answers are wrong as they did not ask for the vectors to be unit vectors.

The other thing you asked about, PQ with both an arrow above it and a caret (or hat, for a unit vector), is unusual notation, in my experience. Usually, one or the other is used, but not both.

The only vectors which are parallel to a given vector and which are of the same length as that vector are that vector itself and its negative.

I wonder if the answer was cut off and the unit vectors were multiplied in the final step that is not shown?

Thank you for your replies @Mark44, @pasmith and @FactChecker !

No @Mark44 that is was the only the solution published by the lecturer.

I checked the solution again @FactChecker, and nothing was cut-off, it was just the answer to part (c) of the question.

Many thanks!