Finding Velocities of Two Points on a Ladder at a 60-Degree Angle

[karkas]

Homework Statement

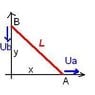
A ladder is at a 60degree angle with a wall and is let to go down. We have to find the velocity of the point that touches the wall(B) and the point that touches the floor(A). Note that we have only completed vectors so no forces are probably to be taken into consideration.

Homework Equations

u(a)=dx(a)/dt and u(b)=dx(b)/dt.

The Attempt at a Solution

Is it possible to find the velocities or am I missing a clue?So far tried a lot of things but can't find them.

It appears that x(b)/x(a) = sqrt(3). Is there maybe a link between the 2 velocities that I'm missing?

 

[ehild]

Make a coordinate system with x-axis along the floor and the y-axis along the wall. The length of the ladder is L and y^2+x^2=L^2.

Take the time derivative of this equation. Use that dx/dt= u(a) and dy/dt=u(b). Find the relation between u(a) and u(b) in terms of x/y. You have found already that x/y = sqrt(3).

ehild

 

[karkas]

Make a coordinate system with x-axis along the floor and the y-axis along the wall. The length of the ladder is L and y^2+x^2=L^2.

Take the time derivative of this equation. Use that dx/dt= u(a) and dy/dt=u(b). Find the relation between u(a) and u(b) in terms of x/y. You have found already that x/y = sqrt(3).

ehild

Well since the time I posted I have done quite some studying and thought of a way to solve the problem, although highly uncertainly. I have turned the ladder into a vector r and written :

dr/dt=dr(x)/dt * x + dr(y)/dt * y = u(x)*x + u(y)*y (1)

The derivative of the vector will be as shown and known: dr/dt = dθ/dt * η where
η=cos(90-θ)*x + sin(90-θ)*y = sinθ*x + cosθ*y (2)

therefore u(x)=dθ/dt * sinθ and u(y)=dθ/dt * cosθ.Where am I wrong??

(forgot to say I really appreciate your help ehild, given the time!)

 

[ehild]

You have two points which move along the axes. The position vectors are $\vec {r_a}=x_a \hat x$ and $\vec {r_b}=y_b \hat y$, the velocity vectors are $\vec {u_a}=u(a)\hat x$ and $\vec {u_b}=u(b) \hat y$.

The length of the ladder is L, which does not change during the motion so its time derivative is zero. $x_a^2+y_b^2=L^2$, so

$2x_a dx_a/dt +y_b dy_b/dt =0$, that is

$x_a u(a) +y_b u(b) =0$

ehild

 

[karkas]

You have two points which move along the axes. The position vectors are $\vec {r_a}=x_a \hat x$ and $\vec {r_b}=y_b \hat y$, the velocity vectors are $\vec {u_a}=u(a)\hat x$ and $\vec {u_b}=u(b) \hat y$.

The length of the ladder is L, which does not change during the motion so its time derivative is zero. $x_a^2+y_b^2=L^2$, so

$2x_a dx_a/dt +y_b dy_b/dt =0$, that is

$x_a u(a) +y_b u(b) =0$

ehild

Yes with the exception of the L factor that I added a while ago the equations I have derived seem correct, and come from the equations that you have presented, I derived them in a different fashion. I guess I didn't know what I was supposed to take for granted. There's no way to know the velocities without the functions for x and y then, right? Thanks again.

 

[ehild]

You can find the ratio of the velocities at the given angle.
It is not clear what the question is. If you have two find the velocities as functions of time, you need to use some Physics. Newton's laws, force and torque, moment of inertia.

ehild

 

[karkas]

You can find the ratio of the velocities at the given angle.
It is not clear what the question is. If you have two find the velocities as functions of time, you need to use some Physics. Newton's laws, force and torque, moment of inertia.

ehild

Yea you're right. I guess the teacher wanted the ratio, he wasn't very clear I guess. Anyway problem solved!