member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For this,
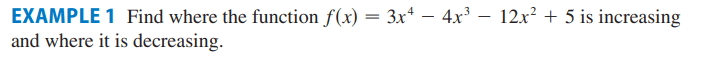
I first try to work out where function is increasing
My working is
##f'(x) = 12x^3 - 12x^2 - 24x##
For increasing,
##12x(x^2 - x - 2) > 0##
##12x > 0## and ##(x - 2)(x + 1) > 0##
##x > 0## and ##x > 2## and ##x > -1##
However, how do I combine those facts into a single domain restriction? Do you just say f(x) increaseing for ##x > - 1##?
Many thanks!
I first try to work out where function is increasing
My working is
##f'(x) = 12x^3 - 12x^2 - 24x##
For increasing,
##12x(x^2 - x - 2) > 0##
##12x > 0## and ##(x - 2)(x + 1) > 0##
##x > 0## and ##x > 2## and ##x > -1##
However, how do I combine those facts into a single domain restriction? Do you just say f(x) increaseing for ##x > - 1##?
Many thanks!