Finding x: Graphical Solution to sin(x/2)=x/4

[garyng2001hk]

Homework Statement

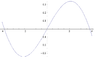
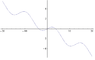
Solve for x.

Homework Equations

Given sin(x/2) = x/4.

The Attempt at a Solution

no idea. the question gives a hint: use graphical method.

 

[icystrike]

You just have to graph y=sin(x/2) and y=x/4 and find the intersection pts.

 

[alijav]

your solution comes as mentioned below

1. draw a curve of x vs sin(x/2)
2. draw a second curve of "x vs x/4"

The solution for x is where both the curves intersect. these are two points

x=0
and
x=3.8

you can find the resultant chart in attached file.

 

[SONOS]

Plotting $$\sin(x/2)$$ vs. x and $$x/4$$ is the way to go indeed.

You can plot this another way also.
Rearranging

$$sin(x/2) = x/4$$

to

$$sin(x/2) - x/4 = 0$$

and plotting where the curve crosses the x-axis is also another way. It crosses three times. At exactly x=0 and at x equals approximately -3.8 and approximately +3.8.
Close up you see the "zero-crossings" of the x-axis at {-3.8,0,3.8} and if you zoom out you see the curve does not cross at any other points (as far as we can see).

 

[SONOS]

Here it is from very far away.