- #1
pavadrin
- 156
- 0
Hey
I have recently been studying for my upcoming exams. I am stuck on the following problem involving radians. Here is the diagram for it.
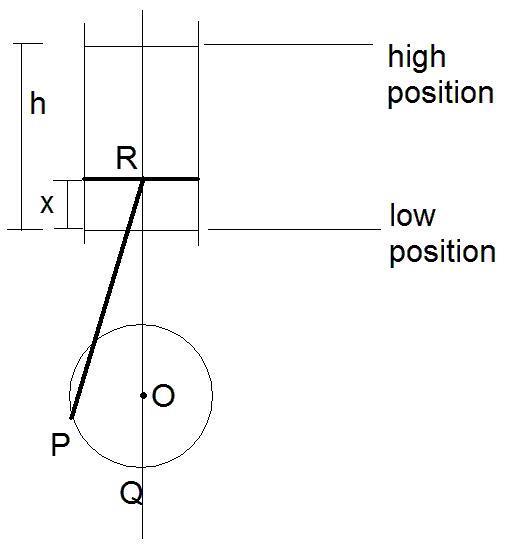
Where PQ = the radius of the circle
I need to find x in as a percentage in terms of h
My working for this problem is as follows
in a circle there is 2pi radians, therefore in half a cirlce there is pi radians, which means for that for pi radians the pistion moves for the high position to the low posotion.
I then calculated the remainder of the angle in half a circle to determine how much the piston had moved, which resulted in being 2.1416 radians.
I then calculated this as a percentage by dividing it by pi and multiply it by 100, which gave me an answer of 68% (correct to one decimal place)
Form here I took that value, 68% from 100% which gave me an answer as being 32% which I assumed as being the value for x.
However I checked the answer in the back of the book and it said 17%.
Could someone please tell me where I have gone wrong? Or if the answer in the book is wrong?
Thanks in advance,
Pavadrin
I have recently been studying for my upcoming exams. I am stuck on the following problem involving radians. Here is the diagram for it.
Where PQ = the radius of the circle
I need to find x in as a percentage in terms of h
My working for this problem is as follows
in a circle there is 2pi radians, therefore in half a cirlce there is pi radians, which means for that for pi radians the pistion moves for the high position to the low posotion.
I then calculated the remainder of the angle in half a circle to determine how much the piston had moved, which resulted in being 2.1416 radians.
I then calculated this as a percentage by dividing it by pi and multiply it by 100, which gave me an answer of 68% (correct to one decimal place)
Form here I took that value, 68% from 100% which gave me an answer as being 32% which I assumed as being the value for x.
However I checked the answer in the back of the book and it said 17%.
Could someone please tell me where I have gone wrong? Or if the answer in the book is wrong?
Thanks in advance,
Pavadrin