Finite expansion of a fraction of functions

[Cha0t1c]

I am having a problem finding the right order above and below to find the finite expansion of a fraction of usual functions assembled in complicated ways. For instance, a question asked to find the limit as x approaches 0 for the following function

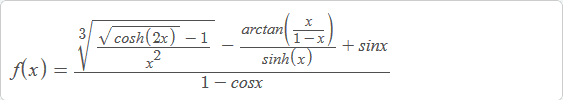
I know that to solve it we must first find the finite expansion near 0 then apply the limit. I also know that, I must first find the finite expansion of the numerator and the denominator then then apply the Euclidean division to find the final answer. However, what I still fail to do correctly is to determine the order for each element so that the final polynomial would assume an order of 3 or 4 for example. Help me please!

 

[Gaussian97]

Well, my advice is:
Do the series expansion of each element up to a certain order (whatever you want). But keep always in mind what terms are you neglecting, I would write, for example, $e^x = 1 + x + O(x^2)$. Notice that this equation is exact, not an approximation, so doing that you can go through the entire calculation and obtain the final result.
You can do some previous analysis at the beginning to know more or less when to stop in the expansion, but if this is not clear for you now, I would recommend you to star by try and error.

 

[Cha0t1c]

Thanks for the answer. Yeah, it seems like the best way to become better at this is to practice until I develop an intuition for such problems. I also have an additional question, should the orders of o(x^n) be all equal? Let's say I write the expansion of e^x to order of 2 and cosx to order of 4.What should I do in this case? Keep the o(x2) for e^x and o(x4) for cosx or perhaps put both as o(x4)?

 

[Gaussian97]

You can expand all the function to any order, remember that $O(x^2)$ means something that is of order $x^2$ or higher, so you can think of this $O(x^n)$ as polynomials of order n, therefore if you sum a polynomial of order $x^2$ plus a polynomial of order $x^4$ you get a polynomial of order $x^2$. So if you have something like
$$(1+x+O(x^2))+(1-x+x^2+O(x^3))=$$$$(1+1)+(1-1)x+(O(x^2)+x^2+O(x^3))=2+O(x^2)$$
Notice that although we know the second order in the second function, it's useless because we don't know the second-order term of the first function

 

[mathman]

For this particular problem, the first term in the denominator is $\frac{x^2}{2}$. Numerator terms therefore don't need any higher order terms.

 

[Gaussian97]

For this particular problem, the first term in the denominator is $\frac{x^2}{2}$. Numerator terms therefore don't need any higher order terms.

Yes, but if you expand all the function to order 2 you will not get the correct answer.

 

[mathman]

Yes, but if you expand all the function to order 2 you will not get the correct answer.

Should get correct answer if done properly. For starters the numerator of term inside the cube root has to be expanded to order 8.

 

[Gaussian97]

Should get correct answer if done properly. For starters the numerator of term inside the cube root has to be expanded to order 8.

Well, depending on what do you mean with "should get the correct answer if done properly", if you expand all the function to second-order the best thing you can do is to say that this limit is of order $O(x^0)$, i.e, that it's not infinite, which is good but, not if you want the exact value for the limit.

Also, to get the correct limit is enough to expand to order 4.

 

[mathman]

Well, depending on what do you mean with "should get the correct answer if done properly", if you expand all the function to second-order the best thing you can do is to say that this limit is of order $O(x^0)$, i.e, that it's not infinite, which is good but, not if you want the exact value for the limit.

Also, to get the correct limit is enough to expand to order 4.

The numerator within the cube root has to expand to include $x^8$ term. Then the cube root arg. is up to $x^6$, so that after cube root it is up tp $x^2$ matching the denominator.

 

[Gaussian97]

Not really, because the term inside the cubic root doesn't have limit zero, it has limit one, and therefore you can't use Taylor's polynomial at $x=0$, but you need the expansion $$\sqrt[3]{1+x}=1+\frac{x}{3}-\frac{x^2}{9}$$so you only need to expand to fourth-order (you can try it and you will see you get the correct answer). It's for this kind of subtilities that I told to Cha0t1c to do it by try and error because all these arguments are very trivial once you have some intuition, but might be very confusing at the beginning.

 

[zinq]

The denominator 1-cos(x) approaches 0 as x approaches 0. If the numerator also approaches 0, then this limit is ripe for applying l'Hopital's rule. This would probably be easier than determining terms of a power series expansion for numerator and denominator.

 

[Gaussian97]

The denominator 1-cos(x) approaches 0 as x approaches 0. If the numerator also approaches 0, then this limit is ripe for applying l'Hopital's rule. This would probably be easier than determining terms of a power series expansion for numerator and denominator.

Well... I disagree, the numerator is very tedious to differentiate (you have root inside functions inside roots so you need to use chain rule multiple times and also there are a lot of fractions etc...), and then you have to differentiate the derivative because you need to use l'Hôpital two times, I really doubt that this limit was supposed to be done using l'Hôpital. Of course, this may be a subjective question, but I think is REALLY much faster use Taylor series here.