Finite square well ##\psi(x)## solution for ##-a < x < a##

[gfd43tg]

Hello, in Griffith's section on the Finite Square Well, $\psi(x)$ (what is the name of this anyway?, I know $\Psi(x,t)$ is called the wave function but how do I call just $\psi(x)$?)

Anyways,

The solution is

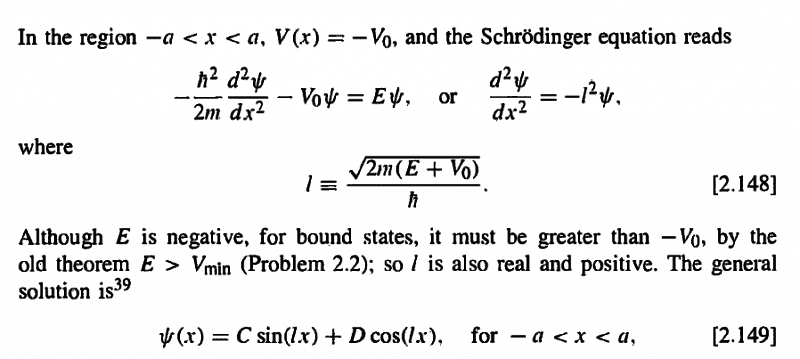
For x < a and x > a, the terms that are infinite as x approaches infinity are said to be not physical, so the author concludes that they are not part of the solution, however that should not be the case here.

Then he clumps all the solutions together

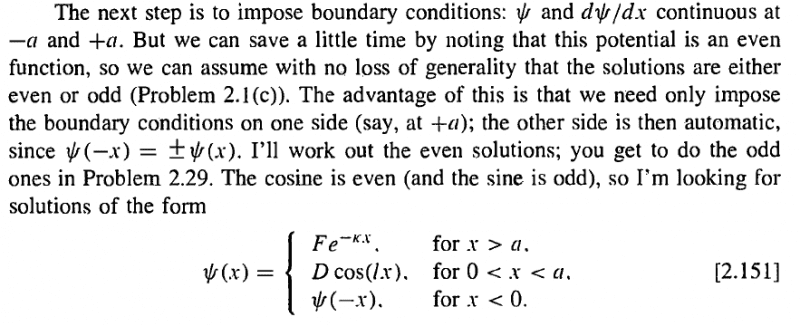
But what happened to the sine term in the region 0 < x < a??

 

[matteo137]

$\Psi(x,t)$ is a time-depemdent wave function, $\psi(x)$ is a time-independent wave function / stationary state.

Since the Schroedinger equation is linear, if you have a solution of the type $\psi(x) = \phi_1(x) + \phi_2(x)$, you can study the two $\phi_i(x)$ separately, and then recombine the results. It is true that the full, general, solution is the one with sine and cosine, but to understand the physics it's enough to work out the rest of the calculations just for one of the two, which simplifies the math. If you try to redo the calculations with the sine, you will see that Eq.[2.154] will become $k = - l \cot(la)$ , ...