MHB Firedawn's questions at Yahoo Answers regarding minimizing cost of pipeline

[MarkFL]

Here is the question:

Calc - Optimization? Confusing question...?


I don't understand what this question is asking:
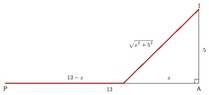
A pipeline needs to be connect from a powerhouse to an island. The island is 5 km away from the nearest point, A on a straight shore line. The powerhouse is 13 km away from point A. If it costs 1.4 times as much to lay the pipeline underwater as it does over land, how should the pipe be laid to minimize the cost?

The ans is 5.1 km from A.

What is this question asking me? I'm so confused.
How would I approach this?

I have posted a link there to this thread so the OP can view my work.

 

[MarkFL]

Hello Firedawn,

Let's first draw a diagram of the path of the pipeline. All distances are in kilometers.

View attachment 1754

The powerhouse is at $\text{P}$, and the island is at $\text{I}$. The path of the pipeline is drawn in red. Let $C$ be the cost to lay the pipeline over land. The total cost is the cost per unit length time the total length, hence we may express the total cost as a function of $x$ as follows:

$$C(x)=C(13-x)+\frac{7}{5}C\sqrt{x^2+5^2}$$

Differentiating with respect to $x$ and equating the result to zero, we obtain:

$$C'(x)=-C+\frac{7}{5}C\frac{x}{\sqrt{x^2+5^2}}=0$$

Multiply through by $$\frac{5\sqrt{x^2+5^2}}{C}$$

$$-5\sqrt{x^2+5^2}+7x=0$$

$$7x=5\sqrt{x^2+5^2}$$

Square both sides:

$$49x^2=25x^2+625$$

$$x^2=\frac{625}{24}$$

Take the positive root:

$$x=\frac{25}{12}\sqrt{6}\approx5.10310363079829$$

To determine the nature of the extremum associated with this critical value, we may use the second derivative test:

$$C'(x)=-C+\frac{7}{5}C\frac{x}{\sqrt{x^2+5^2}}=0$$

$$C''(x)=0+\frac{7}{5}C\frac{\sqrt{x^2+5^2}(1)-x\left(\dfrac{x}{\sqrt{x^2+5^2}} \right)}{\left(\sqrt{x^2+5^2} \right)^2}=\frac{35C}{\left(x^2+5^2 \right)^{\frac{3}{2}}}$$

We see that for all real $x$ the second derivative is positive, hence our critical value is at the global minimum.