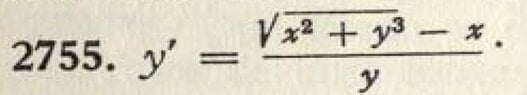Chipset3600
- 79
- 0
Hello, can you guys help me please with this differential equation from Demidovitch book, is to find the solution transforming to polar coordinates :
View attachment 1479
View attachment 1479
Attachments
Last edited: