First-Order Transients: Steady-State DC Response

[dudforreal]

Homework Statement

In the circuit shown below the current source has been switched on for a very long time. Find the DC current in the inductor and the DC voltage across the capacitor.

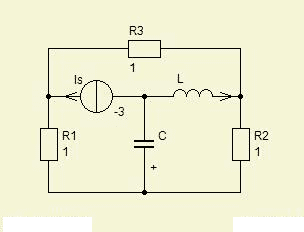
The attempt at a solution

I replaced the inductor and the capacitor with a short circuit and open circuit respectively but after that I don't know what to do.

 

[gneill]

If the capacitor is open, then what current must be passing through the inductor short-circuit?

The circuit becomes a current supply driving two parallel branches. What's the voltage across the branches? What then is the voltage across R2?

 

[dudforreal]

I'm not quite sure what you said but are you saying that I have to use node voltages because last time I did it the answer didn't quite work out.

 

[gneill]

I'm not quite sure what you said but are you saying that I have to use node voltages because last time I did it the answer didn't quite work out.

You can use whatever circuit analysis method you're comfortable with. I only stated what I see as the circuit topology: one current source in parallel with two resistor branches.

You can determine the current in each branch and hence the voltage across R2, or you can find the net resistance and the voltage across the parallel branches and then find the voltage across R2 treating R2 and R1 as a voltage divider. It's up to you how to proceed...

 

[dudforreal]

I used the current divider for the inductor and the voltage divider for the capacitor but I got the answer wrong and I'm quite sure that I got the equations right.

 

[gneill]

Show your work!

 

[dudforreal]

Using the current divider rule for the inductor current -I*(R2+R3/R1+R2+R3) I get 3*(2/3) which is 2A and using ohms law for capacitor voltage -I*(R1*R2/R1+R2+R3) I get 3(1/3) which is 1V.

 

[gneill]

It looks to me like the current from the supply is ALL flowing through the inductor. No divider math required.

I'm not sure that I follow your "ohms law" for the capacitor voltage, but the result, 1V, looks good.

 

[dudforreal]

so how would you get the inductor current?

 

[dudforreal]

...and what method would you use to get the capacitor voltage?

 

[gneill]

After a long time the capacitor looks like an open circuit and the inductor a short circuit, as you previously noted. A circuit diagram revised to reflect this would put the current source in series with the inductor (or its 'wire' replacement). There is no choice other than that the current source's current all flow through the inductor.

For the capacitor voltage I would look at the circuit and note that R2 is in parallel with the capacitor when the inductor is "gone". Thus whatever voltage is across R2 will be the voltage across the capacitor. Either use current divider method to find the current through R2 (and then Ohm's Law for the voltage). or find the voltage across both branches via the net resistance and current, and then apply the voltage divider rule for the voltage across R2. Choose the method that suits you.

 

[dudforreal]

Can you show your work I'm still a bit confused about your method.

 

[gneill]

Can you show your work I'm still a bit confused about your method.

Sorry, but I can't do that. I can't do the work for you. This is Forums policy. I can only help you with your own work, offer suggestions, hints, and so on.

What I can do is redraw the circuit slightly to see if it gives you any ideas. Here it is rotated so that the current supply is vertical and moved from between the resistor branches (this is allowed because they are all in parallel and the order doesn't matter). I've left the "ghost" of the capacitor in place.

As you can see, the potential across the capacitor will be the same as that of R2. Can you solve for it?

 

[dudforreal]

I get the equivalent resistance as 3 ohms and multiply it by current to get a voltage of 9V.

 

[gneill]

I get the equivalent resistance as 3 ohms and multiply it by current to get a voltage of 9V.

Check your equivalent resistance. What's in series and what's in parallel?

 

[dudforreal]

Oh... so is R2 and R1 parallel with each other and then the equivalent resistance of R2 and R1 are in series with R3?

 

[gneill]

Oh... so is R2 and R1 parallel with each other and then the equivalent resistance of R2 and R1 are in series with R3?

No, the other way around. R1 and R2 are in series with each other.

 

[dudforreal]

Then the equivalent resistance of R2 and R1 is parallel with R3 which gives an overall equivalent resistance of 2 ohms and a voltage of 6V.

 

[gneill]

Then the equivalent resistance of R2 and R1 is parallel with R3 which gives an overall equivalent resistance of 2 ohms and a voltage of 6V.

R1 + R2 = 2 Ohms. 2 Ohms in parallel with 1 Ohm is ...?

 

[dudforreal]

oh sorry so the equivalent resistance is 0.667 ohms which gives a voltage of 2V.

 

[gneill]

oh sorry so the equivalent resistance is 0.667 ohms which gives a voltage of 2V.

Ah! Now we're getting somewhere

So the voltage across R2 will be...?

 

[dudforreal]

ok so now the voltage across R2 is 2 x 1 = 2V which is the voltage across the capacitor.

 

[gneill]

ok so now the voltage across R2 is 2 x 1 = 2V which is the voltage across the capacitor.

No, you'll need to use the voltage divider equation; R2 and R1 are in series, with 2V total across them. What's the voltage divider equation for two resistors in series?

 

[dudforreal]

2(1/2) = 1V across the capacitor?

 

[gneill]

2(1/2)?

Yes, or in symbols, the voltage across R2 is:

V_{R2} = V_{in} \frac{R2}{R1 + R2}

 

[dudforreal]

ok so the inductor current would just be 3A right?

 

[gneill]

ok so the inductor current would just be 3A right?

That's what the circuit shows. You should be able to see that from the circuit diagram; when the capacitor is "gone", the current source is connected in series with the inductor. So it MUST carry all the source's current.

 

[dudforreal]

...the voltage across the capacitor = the voltage across R2 = 1V. Am I right?

 

[gneill]

...the voltage across the capacitor = the voltage across R2 = 1V. Am I right?

Are you guessing? Can you present justification? Also, be sure to check with the circuit diagram to make sure that you get the required polarity for the voltage on the capacitor if they've indicated a preferred orientation for its measurement.

 

[dudforreal]

I thought the voltage across the capacitor must be the same as the voltage across R2.

 

[gneill]

I thought the voltage across the capacitor must be the same as the voltage across R2.

Well, you asked, so I thought perhaps you were contemplating other thoughts on the matter.

The circuit diagram clearly shows that at steady state the capacitor is effectively in parallel with R2 (the inductor is a short).

 

[dudforreal]

...so the capacitor voltage is 1V?

 

[gneill]

...so the capacitor voltage is 1V?

Do you have a better suggestion?

{I have to say that I don't like providing answers to questions framed as guesses; they're too much like fishing for a result rather than understanding. I tend to turn such questions back on the poser automatically. Sorry if it seems brusk.}