MHB Floor Function Equation?

[Jameson]

Thank you to MarkFL for this problem!

Solve the following equation:

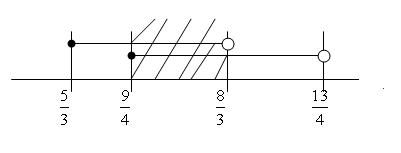
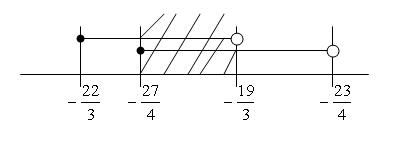
$\displaystyle \left\lfloor x+\frac{7}{3} \right\rfloor^2+\left\lfloor x-\frac{9}{4} \right\rfloor=16$

Note: $\displaystyle \lfloor x \rfloor$ denotes the largest integer not greater than $x$. This function, referred to as the floor function, is also called the greatest integer function, and its value at $x$ is called the integral part or integer part of $x$.
--------------------

 

[Jameson]

Congratulations to the following members for their correct solutions:

1) anemone

The following members submitted partially correct solutions:

1) Sudharaka

Solution (from anemone):

Spoiler

Since the given equation is a quadratic equation, we are expecting to find two solutions and since floor function is involved, the solutions must be in a range of some numbers.

Bearing this in mind, I noticed that if I let $$\left\lfloor x+\frac{7}{3} \right\rfloor=4$$ and $$\left\lfloor x-\frac{9}{4} \right\rfloor=0$$ then I would get $$\left\lfloor x+\frac{7}{3}\right\rfloor^2+\left\lfloor x-\frac{9}{4}\right\rfloor=16$$ and hence obtained the first set of solutions.

To find the region where all of the coordinates of that region satisfy both conditions $$\left\lfloor x+\frac{7}{3} \right\rfloor=4$$ and $$\left\lfloor x-\frac{9}{4} \right\rfloor=0$$ simultaneously, we do as follows:

[TABLE="class: grid, width: 500"]
[TR]
[TD]$$\left\lfloor x+\frac{7}{3} \right\rfloor=4$$[/TD]
[TD]$$\left\lfloor x-\frac{9}{4} \right\rfloor=0$$[/TD]
[/TR]
[TR]
[TD]$$4\le x+\frac{7}{3}<5$$[/TD]
[TD] $$0\le x-\frac{9}{4}<1$$[/TD]
[/TR]
[TR]
[TD]$$\frac{5}{3}\le x< \frac{8}{3}$$[/TD]
[TD]$$\frac{9}{4}\le x< \frac{13}{4}$$[/TD]
[/TR]
[/TABLE]



Hence, the first solution set that we found is $$\frac{9}{4}\le x<\frac{8}{3}$$.

I repeat the process to find the second solution set by considering the negative value of $$x$$ and this leads me to assume the cases $$\left\lfloor x+\frac{7}{3} \right\rfloor=-5$$ and $$\left\lfloor x-\frac{9}{4} \right\rfloor=-9$$ then I would get the $$\left\lfloor x+\frac{7}{3}\right\rfloor^2+\left\lfloor x-\frac{9}{4}\right\rfloor=25-9=16$$ and hence get one of the set of solutions.

[TABLE="class: grid, width: 500"]
[TR]
[TD]$$\left\lfloor x+\frac{7}{3} \right\rfloor=-5$$[/TD]
[TD]$$\left\lfloor x-\frac{9}{4} \right\rfloor=-9$$[/TD]
[/TR]
[TR]
[TD]$$-5\le x+\frac{7}{3}<-4$$[/TD]
[TD] $$-9\le x-\frac{9}{4}<-8$$[/TD]
[/TR]
[TR]
[TD]$$-\frac{22}{3}\le x< -\frac{19}{3}$$[/TD]
[TD]$$-\frac{27}{4}\le x< -\frac{23}{4}$$[/TD]
[/TR]
[/TABLE]



This gives me the second solution set $$-\frac{27}{4}\le x<-\frac{19}{3}$$.

Therefore, $$-\frac{27}{4}\le x<-\frac{19}{3}$$ and $$\frac{9}{4}\le x<\frac{8}{3}$$ are the solution sets to this problem.

Here are also two additional methods for solving this from the person who submitted the problem, MarkFL. :)

Spoiler

Method 1:

We may choose to set (where $n\in\mathbb{Z}$):

$\displaystyle n\le x+\frac{7}{3}<n+1$

so that:

$\displaystyle \left \lfloor x+\frac{7}{3}\right \rfloor^2=n^2$

So now our equation is:

$\displaystyle n^2+\left \lfloor x-\frac{9}{4}\right \rfloor=16$

$\displaystyle 16-n^2=\left \lfloor x-\frac{9}{4}\right \rfloor$

and this gives us:

$\displaystyle 16-n^2\le x-\frac{9}{4}<16-n^2+1$

$\displaystyle 16-n^2\le x-\frac{9}{4}<17-n^2$

We may simplify the system as:

$\displaystyle n-\frac{7}{3}\le x<n-\frac{4}{3}$

$\displaystyle \frac{73}{4}-n^2\le x<\frac{77}{4}-n^2$

We now have two intervals where $x$ must be, and since $x$ must simultaneously satisfy both inequalities, we want to find the intersection of these two intervals, or where they overlap. In order for there to be any overlap, we require the lower bound of each interval to be less than or equal to the upper bound of the other, giving us:

$\displaystyle n-\frac{7}{3}\le\frac{77}{4}-n^2\:\therefore\:n^2+n-\frac{259}{12}\le0$

and

$\displaystyle \frac{73}{4}-n^2\le n-\frac{4}{3}\:\therefore\:0\le n^2+n-\frac{235}{12}$

For $\displaystyle n^2+n-\frac{259}{12}\le0$ we find, by equating the quadratic to zero to find its roots:

$\displaystyle n=\frac{-3\pm\sqrt{786}}{6}$

So, using decimal approximations, $n$ must be greater than about $-5.1726$ and less than about $4.1726$.

For $\displaystyle 0\le n^2+n-\frac{235}{12}$ we find, by equating the quadratic to zero to find its roots:

$\displaystyle n=\frac{-3\pm\sqrt{741}}{6}$

So, using decimal approximations, $n$ must be less than about $-4.9535$ and greater than about $3.9535$.

So, we find the only integer solutions for $n$ are $-5$ and $4$.

Case 1:

$\displaystyle n=-5$

$\displaystyle -\frac{22}{3}\le x<-\frac{19}{3}$

$\displaystyle -\frac{27}{4}\le x<-\frac{23}{4}$

Thus:

$\displaystyle -\frac{27}{4}\le x<-\frac{19}{3}$

Case 2:

$\displaystyle n=4$

$\displaystyle n-\frac{7}{3}\le x<n-\frac{4}{3}$

$\displaystyle \frac{73}{4}-n^2\le x<\frac{77}{4}-n^2$

$\displaystyle \frac{5}{3}\le x<\frac{8}{3}$

$\displaystyle \frac{9}{4}\le x<\frac{13}{4}$

Thus:

$\displaystyle \frac{9}{4}\le x<\frac{8}{3}$

So, the solution for $x$ in interval notation is:

$\displaystyle \left[-\frac{27}{4},-\frac{19}{3} \right)\,\cup\,\left[\frac{9}{4},\frac{8}{3} \right)$

Method 2:

The first step is to reduce the floor arguments using:

$\displaystyle \lfloor x\pm(n+k) \rfloor=\lfloor x\pm k \rfloor\pm n$ where $\displaystyle n\in\mathbb N$ and $\displaystyle k\in\mathbb R$, $0<k<1$.

So now we have:

$\displaystyle \left(\left\lfloor x+\frac{1}{3}\right\rfloor +2\right)^2+\left\lfloor x-\frac{1}{4}\right\rfloor-2=16$

$\displaystyle \left\lfloor x+\frac{1}{3}\right\rfloor^2+4\left\lfloor x+\frac{1}{3}\right\rfloor+
\left\lfloor x-\frac{1}{4}\right\rfloor=14$

Then we observe that:

$\displaystyle d\left(x-\frac{1}{4},x+\frac{1}{3} \right)=\left|\left(x+\frac{1}{3} \right)-\left(x-\frac{1}{4} \right) \right|=\frac{1}{3}+\frac{1}{4}=\frac{7}{12}$

Now since the difference between the two arguments is less than 1 we have to consider two cases. Either the two arguments are between successive integers or the two arguments lie on either side of an integer. In the first case, the smaller argument may be equal to the smaller of the two successive integers but the larger argument must be strictly less than the larger of the two successive integers.

Case 1:

$\displaystyle n\le x-\frac{1}{4}<n+\left(1-\frac{7}{12} \right)$

$\displaystyle n\le x-\frac{1}{4}<n+\frac{5}{12}$

$\displaystyle n+\frac{1}{4}\le x<n+\frac{2}{3}$

Since both arguments are between the same two successive integers, we must have:

$\displaystyle n=\left\lfloor x-\frac{1}{4}\right\rfloor=\left\lfloor x+\frac{1}{3}\right\rfloor$

Our equation becomes:

$\displaystyle n^2+5n-14=0$

$\displaystyle (n+7)(n-2)=0$

Since this equation has integral roots, we may proceed.

First root: $n=-7$

$\displaystyle -7+\frac{1}{4}\le x<-7+\frac{2}{3}$

$\displaystyle -\frac{27}{4}\le x<-\frac{19}{3}$

Second root: $n=2$

$\displaystyle 2+\frac{1}{4}\le x<2+\frac{2}{3}$

$\displaystyle \frac{9}{4}\le x<\frac{8}{3}$

Thus, from the first case, we find the solution for $x$ in interval notation as:

$\displaystyle \left[-\frac{27}{4},-\frac{19}{3} \right)\,\cup\,\left[\frac{9}{4},\frac{8}{3} \right)$

Case 2:

$\displaystyle n=\left\lfloor x-\frac{1}{4} \right\rfloor$

$\displaystyle n+1=\left\lfloor x+\frac{1}{3}\right\rfloor$

And our equation becomes:

$\displaystyle (n+1)^2+4(n+1)+n-14=0$

$\displaystyle n^2+2n+1+4n+4+n-14=0$

$\displaystyle n^2+7n-9=0$

This equation has irrational roots, so there are no valid solutions to consider from this case.