- #1
dylanwalt
- 6
- 4
- Homework Statement
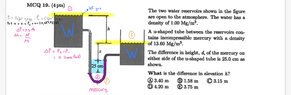
- The two water reservoirs shown in the figure are open to the atmosphere. The water has a density of 1.00 Mg/m°.
A u-shaped tube between the reservoirs contains incompressible mercury with a density of 13.60 Mg/m'.
The difference in height, d, of the mercury on either side of the u-shaped tube is 25.0 cm as shown.
What is the difference in elevation h?
- Relevant Equations
- (delta)P=pg(delta)h
I tried to use this equation, so I isolated the delta h because that is what im solving for and then I thought because the pressure on both ends of the reservoir is both atmospheric pressure the change in pressure is 0. This makes my entire equation 0 and thus height is 0 which is definitely not the case.