Fluid flow inside a cylindrical tank

[fer Mnaj]

Homework Statement

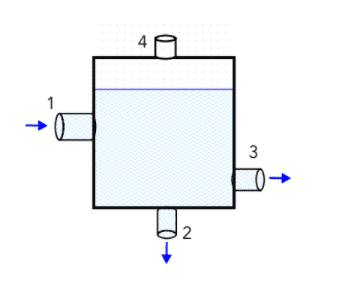
In the interior of a cylindrical tank of diameter: D =24 m,
water flows through a tube 1 with velocity $$v_1 = 20 m/s$$ and exits through
of tubes 2 and 3 with velocities $$v_2 = 8 m/s$$ and $$v_3 = 10 m/s$$ respectively.
In 4 there is a valid vent valve open to atmospheric air.

a) What is the speed with which the water level rises inside the tank?
b) What is the average speed of the air flow in valve 4?

assuming air is incompressible. Suppose
the following pipe diameters: $$D1 = 3 m,
D2 = 2 m, D3 = 2.5 m, D4 = 2 m$$

Relevant Equations

$$A_1v_1=A_2v_2$$
$$P+ρgy+1/2 ρv^2=constant$$

Hi, I´m quite lost and would appreciate guidance

I have solved for 2 tubes using Bernoulli´s equation before, but now how does it change?
Is it really going to rise water level inside? Why?

 

[haruspex]

If the water level stays the same, what can you say about the flows in and out? Is that true of the flows here?

 

[Lnewqban]

If you have the inlet and outlet diameters, you can calculate the cross area of each.
Then, you have the velocities of each flow; therefore you can calculate how much fluid enters and how much exits the tank.

 

[fer Mnaj]

If you have the inlet and outlet diameters, you can calculate the cross area of each.
Then, you have the velocities of each flow; therefore you can calculate how much fluid enters and how much exits the tank.

Indeed:
$$A_1v_1=π(1.5m)^2(20m/s)$$
$$A_2v_2=π(1)^2(8m/s)$$
$$A_3v_3=π(1.25)^2(10m/s)$$

Then we can see that $$Q_1= 141.37 m^3/s$$ is way higher than $$Q_2= 25.13 m^3/s$$ and $$Q_3=49.08 m^3/s$$
So more water enters than exits. In that aspect makes sense.
Now I was thinking to treat tube 2 and 3 as one, could I do that?
How can I proceed to get the rising velocity of water?

 

[gmax137]

This exercise is all about the relationship between area, flowrate, and velocity. You do not need Bernoulli to answer any of the parts.

 

[fer Mnaj]

Indeed:
$$A_1v_1=π(1.5m)^2(20m/s)$$
$$A_2v_2=π(1)^2(8m/s)$$
$$A_3v_3=π(1.25)^2(10m/s)$$

Then we can see that $$Q_1= 141.37 m^3/s$$ is way higher than $$Q_2= 25.13 m^3/s$$ and $$Q_3=49.08 m^3/s$$
So more water enters than exits. In that aspect makes sense.
Now I was thinking to treat tube 2 and 3 as one, could I do that?
How can I proceed to get the rising velocity of water?

So i decided to add $$Q_2$$ and $$Q_3$$, so I would substract them from $$Q_1$$ later.
I thought it would be like a $$Qnet$$, and that would be equal to $$(Atank) (vrise)$$.
Does it make sense?

 

[gmax137]

Does it make sense?

Yes, I think so. Then you can answer part (b) the velocity of the exiting air.

 

[fer Mnaj]

Yes, I think so. Then you can answer part (b) the velocity of the exiting air.

I don´t get that part, does it mean that water is "pushing" the air throughout tube 4? Because continuity equations have worked when we were talking about the same fluid

 

[haruspex]

continuity equations have worked when we were talking about the same fluid

They work for any mix of incompressible fluids. In a given space, such as this tank, the sum of the fluid volumes is constant.
Note you are told to treat the air as incompressible here.