Fluid Force (Real-Life application) Find my error

[Tclack]

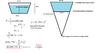
So I'm in the Navy. I work on an aircraft carrier that just went into drydock. The drydock has a large trapezoid door keeping the water out on one side. Our captain wants to know how much force is being held back on that door. I found the dimensions of it and calculated it, but now I'm having doubts.

My work is in the attached document.

I DID keep in mind that the water only goes up 50 feet (though 60ft is the trapezoid's height)
In the end, I got a force of 12.9 million lbs. When I divide by the area of the door (8162sq.ft) I get an average pressure of ~11psi...

14.7 psi is atmospheric pressure telling me that my answer is wrong, but I can't see why! Any thoughts?

 

[SteamKing]

Why do you think your answer is wrong? Is the inside of the drydock evacuated before it is opened?

You have a couple of small errors in your calculations. Seawater weighs 64 lbf/ft^3, so the quantity you call ρ is actually ρ*g. When you first set up your integral to calculate force, the integrand should be 169.5x - (x^2)/4

What you are calculating is the force produced on the dock gate by the seawater alone. Remember, air pressure is present on both sides of the dock gate, so it can be neglected in determining the force acting on the gate from the seawater.

The hydrostatic head acting at the bottom of the dock gate is 50*64/144 = 22.2 psi, so your calculation of 11 psi average pressure seems reasonable.

 

[Tclack]

oh yeah, the 1/4 was in my original paperwork, I just missed copying it down. nice catch.

I guess I'm just confused about this fluid force thing. What is causing the fluid force anyway? If it's just the random movement of the fluid molecules, then the higher the temperature, the more motion, so I would think more fluid force... BUT higher temperature makes the fluid LESS dense and by the equation, LESS force is felt... >o<

 

[Mark44]

I guess I'm just confused about this fluid force thing. What is causing the fluid force anyway? If it's just the random movement of the fluid molecules, then the higher the temperature, the more motion, so I would think more fluid force... BUT higher temperature makes the fluid LESS dense and by the equation, LESS force is felt... >o<

The force that the water exerts on the gate is due to gravity. All of the water molecules "feel" this force, but since water is relatively incompressible, the force acts in all directions. At the top surface of the water, there is no pressure, but as you go deeper, the pressure increases, due to the increasing number of water molecules above that level.

With higher temperature, the water gets less dense, but its volume is increasing. In a confined space, the height of the water has to increase. Keep in mind, though, that near freezing, the volume increases again, as the molecules are rearranged into a crystalline structure.

 

[Tclack]

I'm sorry to keep returning to the atmospheric pressure thing, but. If one square foot was submerged 1 foot underwater (horizontally for simplicity's sake) that would be 1*64/144 = .444... psi. When just before being submerged, the atmosphere was applying 14.7 psi.

Would I add the atmospheric pressure? i.e. 15.1444 psi (for the 1 sq ft. submerged 1 ft)

But the drydock as SteamKing said would be pushed on both sides, cancelling out... right?

 

[SteamKing]

If you want absolute pressure, then the atmospheric pressure must be added. The change in pressure at the bottom of a water column is going to be ρgh or 64*h psf for seawater. Since the atmosphere covers the entire surface of the globe, it can be neglected, unless you are trying to find the pressure acting on a vessel which is either fully or partially evacuated.

 

[Tclack]

Yeah, that's it the "change in pressure" vs. the "absolute Pressure" is what got me.

I suppose I could say that there's 25.7 psi on the drydock wall, but then there's 14.7 psi pushing back, and hence a net average of 11 psi felt along the drydock's Seawater side.

Thank's for the input everyone!