Valour549
- 57
- 4
- Homework Statement
- Water flows steadily through a 3.25-in-diameter pipe and discharges through a 1.25-in-diameter nozzle to atmospheric pressure. The flow rate is 24.5 gpm. Calculate the minimum static pressure required in the pipe to produce this flow rate. Evaluate the axial force of the nozzle assembly on the pipe flange.
- Relevant Equations
- ρQ*V1+P1*A1 = ρQ*V2+P2*A2
Let me start off by saying that I have found (or is given) all of these: ρ, Q, V1, V2, P1, P2, A1, A2 (V being the velocity here). So no problem with Bernoulli or the Continuity equation calculations.
I am just struggling with drawing the FBD in order to evaluate the axial force, Fx
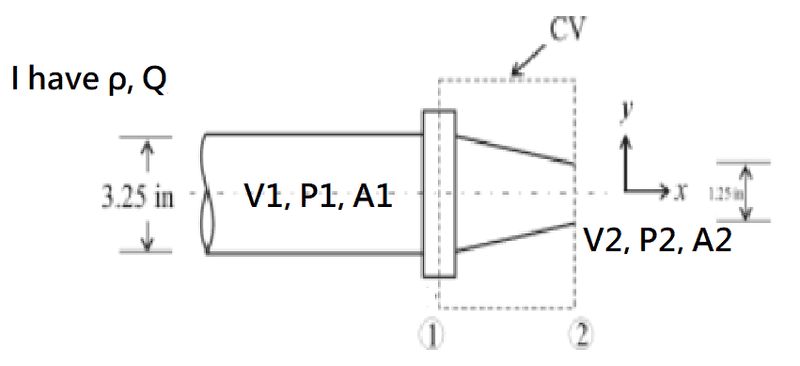
I know we need to write an x-momentum equation to the control volume: ρQ*V1+P1*A1 = ρQ*V2+P2*A2
But I don't know which side the Fx should be added on in the above equation. It says "axial force of the nozzle assembly on the pipe flange", so if I had to guess, Fx would point towards the left. But the bigger problem here is that I'm not even sure whether the terms I have on the LHS (and RHS) causes a force that acts to the left or right of the control volume.
I am just struggling with drawing the FBD in order to evaluate the axial force, Fx
I know we need to write an x-momentum equation to the control volume: ρQ*V1+P1*A1 = ρQ*V2+P2*A2
But I don't know which side the Fx should be added on in the above equation. It says "axial force of the nozzle assembly on the pipe flange", so if I had to guess, Fx would point towards the left. But the bigger problem here is that I'm not even sure whether the terms I have on the LHS (and RHS) causes a force that acts to the left or right of the control volume.