- #1
Bluestribute
- 194
- 0
Homework Statement
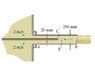
The apparatus or "jet pump" used in an industrial plant is constructed by placing the tube within the pipe. The velocity of the flow within the 200-mm-diameter pipe is 2 m/s, and the velocity of the flow through the 20-mm-diameter tube is V = 37 m/s . The fluid is ethyl alcohol having a density of ρea = 790 kg/m3. Assume the pressure at each cross section of the pipe is uniform. Assume ethyl alcohol is ideal fluid, that is, incompressible and frictionless.
Determine the increase in pressure PB−PA that occurs between the back A and front B of the pipe.
Homework Equations
I'm assuming CoE since it has a pressure term explicitly
The Attempt at a Solution
So I don't really know where to begin. What I have:
Vin = 37 m/s
Vout = 2 m/s
ρ = 790 kg/m3
Ain = π(0.01m)2
Aout = π(0.1m)2
I'm using "in" and "out", but in the end, it's just deltas I'm looking for. But, like . . . I don't know where to begin with these numbers? Do I find kinetic energy? Set that equal to . . . something? Or find a force first. And what to do after that (I'm going to have a lot of questions with CoM and CoE)?