- #1
MrSmit
- 5
- 0
Hello,
I'm a PhD student in medical biology and am doing experiments with bloodvessels. I've modified an existing technique and getting unexpected results (ofcourse..). I think it is due to a pressure difference but my knowledge of physics is inadequate to be sure. Ill give a short explanation of the techniques and then at the end put a hopefully not too difficult question.
The technique I'm using is pressure myography; we cut a small section of a bloodvessel from tissue and attach each end to a glass cannula in a vessel chamber (see image one). The chamber contains fluid (salt solution) and is closed during the experiment. The chamber is not airtight, there are two open ends at the sides but the water from the chamber does not leak from them. Then, the pressure inside the vessel is raised to ~80 mmHg by closing one of the cannulas and attaching a water column to the the other (which is open at the end).
This is the standard situation (situation 1).
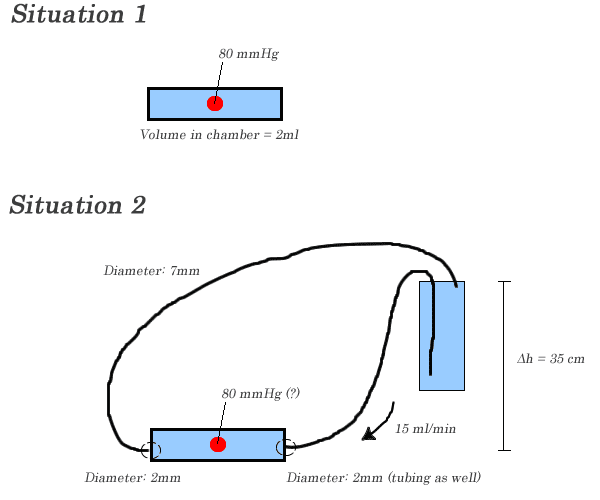
In my modified setup, the fluid inside the chamber is continuously refreshed. Approximately 35cm above the chamber is a fluid reservoir (due to technical reasons). The fluid is then pumped into the chamber by a rolling pump at 15ml/min. The 'excess' volume goes back into the reservoir through a tubing. This is situation two.
My feeling tells me that there is increased pressure, or stress, on the bloodvessel in the second situation. Others however say that the pressure difference between the inside and the outside of the vessel probably becomes smaller and therefore the stress decreases.. I'm definitely in need of someone more experienced in this matter..
My questions are:
- Is there increased pressure in the chamber?
- Is there a possibility that the pressure inside the vessel changes?
- Is there a possibility that the stress on the vessel changes?
Thanks in advance!
Image 1
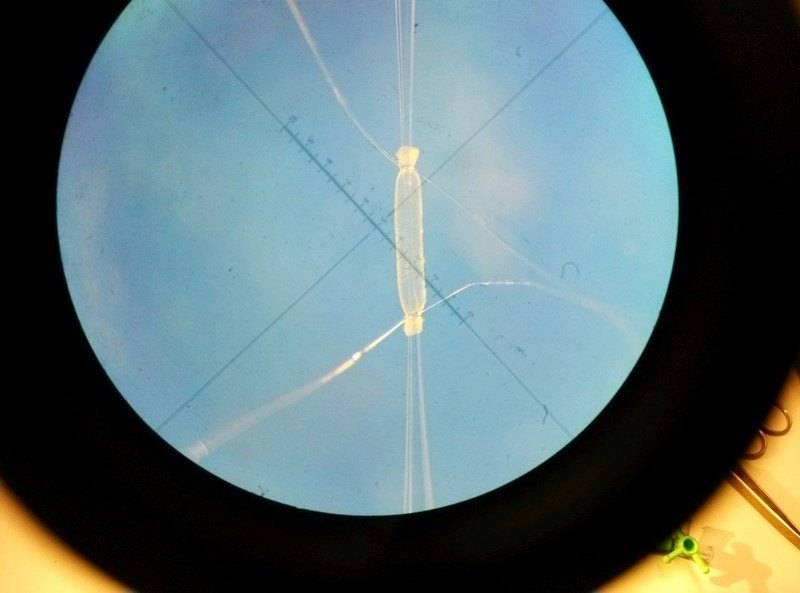
Image 2
I'm a PhD student in medical biology and am doing experiments with bloodvessels. I've modified an existing technique and getting unexpected results (ofcourse..). I think it is due to a pressure difference but my knowledge of physics is inadequate to be sure. Ill give a short explanation of the techniques and then at the end put a hopefully not too difficult question.
The technique I'm using is pressure myography; we cut a small section of a bloodvessel from tissue and attach each end to a glass cannula in a vessel chamber (see image one). The chamber contains fluid (salt solution) and is closed during the experiment. The chamber is not airtight, there are two open ends at the sides but the water from the chamber does not leak from them. Then, the pressure inside the vessel is raised to ~80 mmHg by closing one of the cannulas and attaching a water column to the the other (which is open at the end).
This is the standard situation (situation 1).
In my modified setup, the fluid inside the chamber is continuously refreshed. Approximately 35cm above the chamber is a fluid reservoir (due to technical reasons). The fluid is then pumped into the chamber by a rolling pump at 15ml/min. The 'excess' volume goes back into the reservoir through a tubing. This is situation two.
My feeling tells me that there is increased pressure, or stress, on the bloodvessel in the second situation. Others however say that the pressure difference between the inside and the outside of the vessel probably becomes smaller and therefore the stress decreases.. I'm definitely in need of someone more experienced in this matter..
My questions are:
- Is there increased pressure in the chamber?
- Is there a possibility that the pressure inside the vessel changes?
- Is there a possibility that the stress on the vessel changes?
Thanks in advance!
Image 1
Image 2