- #1
EdTheHead
- 25
- 0
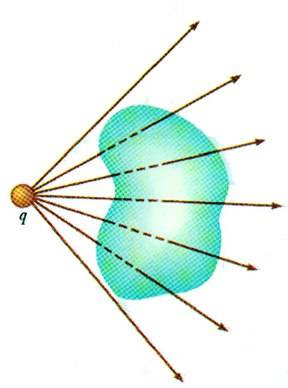
I know that electric flux is defined as the number of electric field lines passing through an area but what kinda area are we talking about. Does it have to be perpendicular to the field lines like this
or could it be at an angle like this
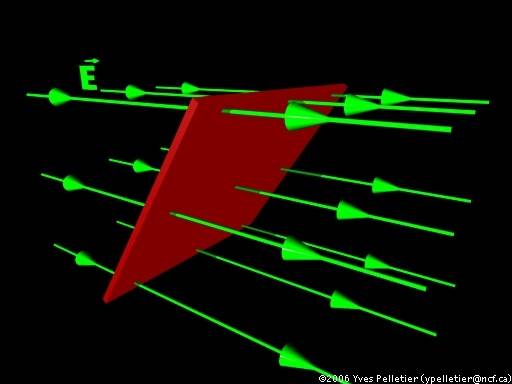
does it have to be a flat area on 1 plane like the previous 2 examples or could it be a 3D area like this
or could it be at an angle like this
does it have to be a flat area on 1 plane like the previous 2 examples or could it be a 3D area like this
Last edited by a moderator: