Snoopey
- 6
- 0
Hi all,
I'm looking for an equation which will give me the focal length of a biconvex lens given that we know both Radii of curvature, the thickness of the lens and the refractive index inside and outside.
An equation is given on wikipedia here http://en.wikipedia.org/wiki/Focal_length as
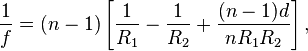
I need something I can reference though and I can't see this equation anywhere else I look. Also I need a more general version of the equation which involves the refractive index of the substance surrounding the lens.
Could anyone point me to a derivation of this formula or lead me in the right direction?
I also need to find a legitimate source for the back focal distance shown on the same page of wikipedia:
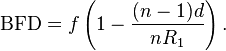
Thanks all!
EDIT: Found what I was looking for, just needed a bit more snooping!
http://physics.tamuk.edu/~suson/html/4323/thick.html
I'm looking for an equation which will give me the focal length of a biconvex lens given that we know both Radii of curvature, the thickness of the lens and the refractive index inside and outside.
An equation is given on wikipedia here http://en.wikipedia.org/wiki/Focal_length as
I need something I can reference though and I can't see this equation anywhere else I look. Also I need a more general version of the equation which involves the refractive index of the substance surrounding the lens.
Could anyone point me to a derivation of this formula or lead me in the right direction?
I also need to find a legitimate source for the back focal distance shown on the same page of wikipedia:
Thanks all!
EDIT: Found what I was looking for, just needed a bit more snooping!
http://physics.tamuk.edu/~suson/html/4323/thick.html
Last edited: