For the friction formula when to use Fn(normal force)×mu and when F×mu

[Iamconfused123]

Homework Statement

When to use for the friction formula; Fn(normal force)×mu and when to use F×mu?
Force F is pushing the object against the wall, will the body move or not?

Relevant Equations

F=ma, Ffr=Fn×mu, Ffr=F×mu

Is there some kind of rule when we are supposed to use Fn×mu compared to F×mu or mg×mu to calculate friction?
Because I don't get the same answer when I use Fn×mu and F×mu. In magnitude the forces are the same but they are not same in directions.
Why is it so?

Here is the photo. Problem goes; will the body(0.5 kg) move when pressed with force F=12 N against wall with static coef. of friction = 0.6.
It won't, but that is not what bothers me.

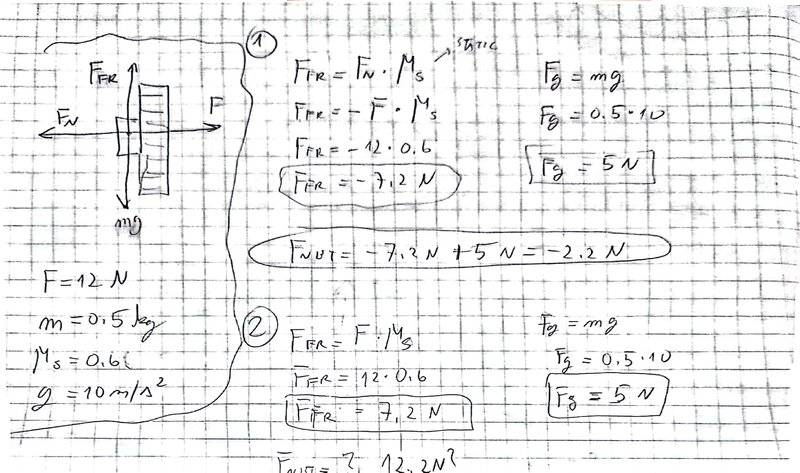
Like I know that for case no.2 I am supposed to subtract, but I wonder why I didn't end up with one force as negative. If we pretend that I don't know that I am supposed to subtract one force from another, how would I end up with -2.2 and not 12.2? Because subtraction is additon of negative number and I don't have any negatives in case no.2.

I know that it's because F and Fn are going in opposite directions and have different signs, but even in most basic problems when calculating Friction force we can use Ffr= Fn×mu or Ffr=mg×mu. And those answers were always the same, or rather I figured that I was subtracting two positives using my knowledge that forces act in opposite direction so it must be subtraction, like, I came to conclusion using intelligence, it didn't conclude itself from math.
So, why is then in textbooks written that Ffr=mg×mu, when in fact is Ffr= Fn × mu.? In magnitude it's the same as Ffr=mg×mu but not in the dirrection.

 

[nasu]

It is always the normal component of the net force acting on the object.

 

[Orodruin]

It is always the normal component of the net force acting on the object.

Noting of course that this is the maximal friction. Friction in a static situation will typically not be equal to normal force x friction coefficient, but rather smaller than that - unless it is really at the limit of slipping.

 

[Iamconfused123]

It is always the normal component of the net force acting on the object.

Oh, didn't know that. Thank you.

But why do people write Fn=mg, when it's not. It's Fn=-mg

Like this for example.

Why didn't he write Fn=-mg insted of Fn=mg. It's the same in my textbook, and I believe I have seen the same expressions elsewhere.

 

[Iamconfused123]

Noting of course that this is the maximal friction. Friction in a static situation will typically not be equal to normal force x friction coefficient, but rather smaller than that - unless it is really at the limit of slipping.

Thanks, I know. But I really appreciate the comment.

 

[Orodruin]

Oh, didn't know that. Thank you.

But why do people write Fn=mg, when it's not. It's Fn=-mg

Like this for example.View attachment 337744
Why didn't he write Fn=-mg insted of Fn=mg. It's the same in my textbook, and I believe I have seen the same expressions elsewhere.

The positive directions of the forces have been specified in the figure. In opposite directions.

 

[Iamconfused123]

The positive directions of the forces have been specified in the figure. In opposite directions.

Ohh, so if we draw a sketch we can just do the algebra?

 

[nasu]

The

Oh, didn't know that. Thank you.

But why do people write Fn=mg, when it's not. It's Fn=-mg

Like this for example.View attachment 337744
Why didn't he write Fn=-mg insted of Fn=mg. It's the same in my textbook, and I believe I have seen the same expressions elsewhere.

The sign of the force component depends on the choice of positive direction. The sign is not relevant for the formula for friction force (static or kinetic) which relates the magnitudes of the two forces (normal and friction).

 

[Orodruin]

I should add: It is quite common to introduce force directions in different directions depending on what you would expect to be the force direction. There is of course nothing wrong with doing so as long as you take the correct sign in the equilibrium equation. If your intuition about the direction was wrong, then the force will simply cone out negative, meaning it is in the opposite direction of what you expected.

Of course, there is also nothing wrong with defining all forces with the same positive direction. The sign will then tell you the actual direction.

 

[Iamconfused123]

I should add: It is quite common to introduce force directions in different directions depending on what you would expect to be the force direction. There is of course nothing wrong with doing so as long as you take the correct sign in the equilibrium equation. If your intuition about the direction was wrong, then the force will simply cone out negative, meaning it is in the opposite direction of what you expected.

Of course, there is also nothing wrong with defining all forces with the same positive direction. The sign will then tell you the actual direction.

Thanks, but just to confirm. If we draw a sketch we can just do the algebra like when we are doing normal math equations?

Because it kind of does not make sense that Fn=mg. If he wrote |Fn|=|mg| then okay. But forces are vectors.

 

[Iamconfused123]

The
The sign of the force component depends on the choice of positive direction. The sign is not relevant for the formula for friction force (static or kinetic) which relates the magnitudes of the two forces (normal and friction).

But shouldn't we then use absolute values for that? |Fn|=|mg|

 

[Orodruin]

If we draw a sketch we can just do the algebra like when we are doing normal math equations?

As long as you take the appropriate signs into account when writing down the equilibrium equation. In your example, weight is defined in the down direction and the normal force in the up direction. The equilibrium equation in the up direction is therefore Fn - W = 0 (not Fn + W = 0) because weight was defined positive in the opposite direction of the direction you are considering. Therefore Fn = W. Since the weight is mg downwards and weight was specified as positive downwards, Fn = mg. Since Fn was specified upwards, Fn is indeed equal to mg upwards.

 

[haruspex]

It is always the normal component of the net force acting on the object.

… do you mean, the normal component of the net of the other forces acting on the object? But that would still be only for statics. For an accelerating body the normal force might not equal that.
I define the normal force, $F_n$, as the minimum reaction force from the contacting body to prevent interpenetration.
Necessarily, the minimum such force will be normal to the contact plane between the bodies. (For corner-on-corner contact the contact plane is indeterminate.)

 

[Orodruin]

Yes. The correct forms are
Static friction: |Fs|≤μs|Fn|
Kinetic friction: |Fk|=μk|Fn|
where the normal force, Fn, is the minimum reaction force from the contacting body to prevent interpenetration.

This was not the question. The question was if it should be $|F_n| = |mg|$ or not. This equation, while true, removes the information about the proper direction of the normal force.

 

[nasu]

… to be more precise, the normal component of the net of the other forces acting on the object. Which leads to another potentially indeterminate case, where the object contacts multiple other bodies.

Other than what?
But yes, for the case of multiple contacts I would say just the normal component of the contact force. It is not the net force.
But thus is going too far from the OP question. Which is the usual way here.

 

[haruspex]

This was not the question. The question was if it should be $|F_n| = |mg|$ or not. This equation, while true, removes the information about the proper direction of the normal force.

Whoops. Thanks, corrected.

 

[haruspex]

Other than what?
But yes, for the case of multiple contacts I would say just the normal component of the contact force. It is not the net force.
But thus is going too far from the OP question. Which is the usual way here.

If the body is not accelerating, the net force on it is zero, so post #2 cannot be what you meant.

 

[nasu]

Oh, other than the force the surface (other object) acts on the body. Yeah, thank you for clarification. I just wondered what you mean. I was not careful in my post.